19. Optimization¶
19.1. Univariate Function Optimization¶
import numpy as np
import matplotlib.pyplot as plt
import math as m
import time # Imports system time module to time your script
plt.close('all') # close all open figures
Here we want to optimize a univariate function:
We first define the function:
def f1simple(x):
# gamma(2,3) density
if (x < 0):
return (0)
if (x == 0):
return (np.nan)
y = np.exp(-2*x)
return (4 * x**2 * y)
Next we define the same function but return \(f(x)\), \(f'(x)\), and \(f''(x)\).
def f1(x):
# gamma(2,3) density
if (x < 0):
return np.array([0, 0, 0])
if (x == 0):
return np.array([0, 0, np.nan])
y = np.exp(-2.0*x)
return np.array([4.0 * x**2.0 * y, \
8.0 * x*(1.0-x)*y, \
8.0*(1 - 4*x + 2 * x**2)*y])
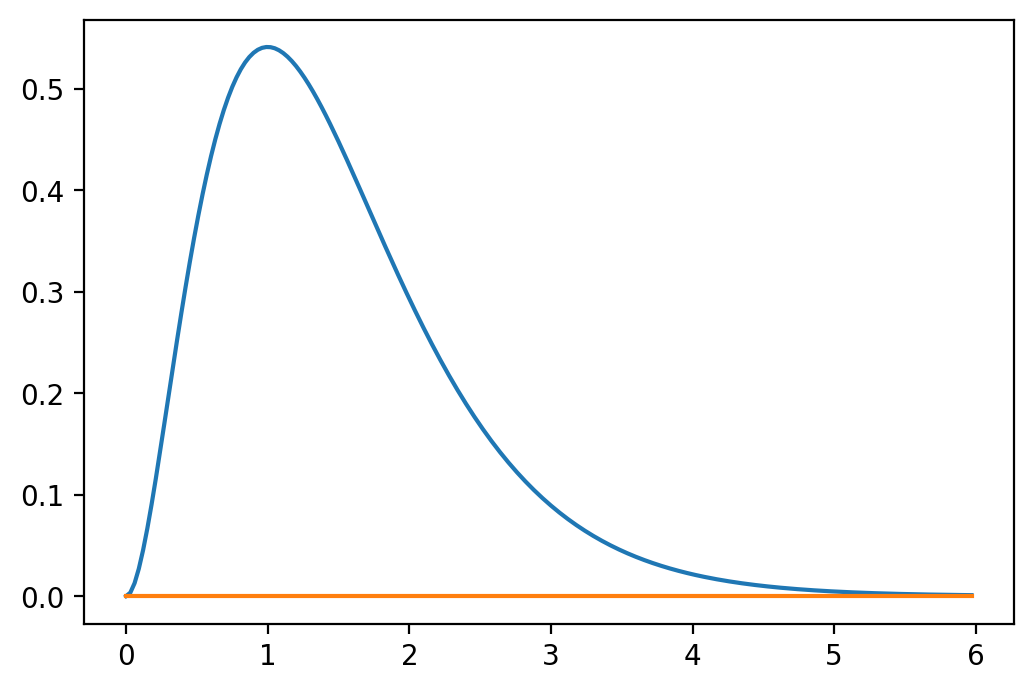
Plotting the function is always a good idea!
xmin = 0.0
xmax = 6.0
xv = np.arange(xmin, xmax, (xmax - xmin)/200.0)
fx = np.zeros(len(xv),float) # define column vector
for i in range(len(xv)):
fx[i] = f1(xv[i])[0]
print("fx[0:10]= ", fx[0:10])
fig, ax = plt.subplots()
ax.plot(xv, fx)
ax.plot(xv, np.zeros(len(xv)))
plt.show()
fx[0:10]= [0. 0.00339035 0.01277165 0.02706275 0.04530976
0.06667364
0.09041885 0.11590306 0.14256769 0.16992939]
19.2. Optimization Methods¶
19.2.1. Newton’s Method¶
In order to implement the Newton method we basically look for the root of a first derivative so that \(f'(x) = 0\).
myOpt = 1.0
fmaxval = f1simple(myOpt)
xmin = 0.0
xmax = 6.0
xv = np.linspace(xmin, xmax, 200)
fx = np.zeros(len(xv),float) # define column vector
for i in range(len(xv)):
fx[i] = f1(xv[i])[0]
fig, ax = plt.subplots()
ax.plot(xv, fx)
ax.plot(xv, fmaxval*np.ones(len(xv)))
ax.axvline(x = myOpt, ymin=0.0, color='r', linestyle='--')
plt.show()
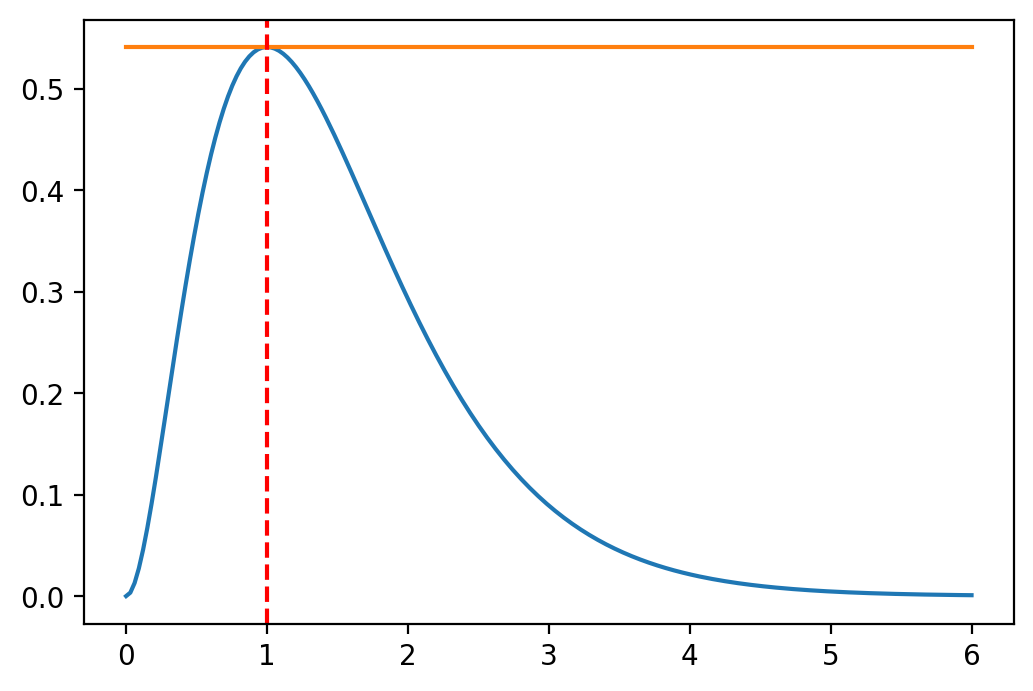
We then use the root finding algorithm from the previous chapter to find this point, or:
Note
Newthon-Raphson Root Finding Algorithm
We have to adjust this of course because the function we search the foot for is already the first derivative of a function, so that we have:
\[x_{n+1} = x_n - \frac{f'(x_n)}{f''(x_n)}\]
def newton(f3, x0, tol = 1e-9, nmax = 100):
# Newton's method for optimization, starting at x0
# f3 is a function that given x returns the vector
# (f(x), f'(x), f''(x)), for some f
x = x0
f3x = f3(x)
n = 0
while ((abs(f3x[1]) > tol) and (n < nmax)):
x = x - f3x[1]/f3x[2]
f3x = f3(x)
n = n + 1
if (n == nmax):
print("newton failed to converge")
else:
return(x)
19.2.2. Golden Section Method¶
The golden-section method works in one dimension only, but does not need the derivatives of the function. However, the function still needs to be continuous. In order to determine whether there is a local maximum we need three points. Then we can use the following:
Note
If \(x_l<x_m<x_r\) and
\(f(x_l) \leq f(x_m)\) and
\(f(x_r) \leq f(x_m)\) then there
must be a local maximum in the interval between \([x_l,x_r].\)
This method is very similar to the bisection method (root bracketing) from the previous section.
The method starts with three starting values and operates by successively narrowing the range of values on the specified interval, which makes it relatively slow, but very robust. The technique derives its name from the fact that the algorithm maintains the function values for four points whose three interval widths are in the ratio
where \(\rho\) is the golden ratio.
In mathematics, two quantities \(a\) and \(b\) are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Assume \(a>b\) then the ratio:
Fig. 19.1 illustrates this geometric relationship.
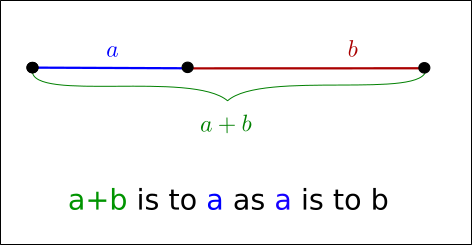
Fig. 19.1 Line segments in the golden ratio¶
The golden ratio is the solution to:
so that
The algorithm proceeds in the following way:
Note
Start with \(x_l<x_m<x_r\) such that
and
and the golden ratio
In the algorithm we then check the following:
If \(x_r - x_l \le \epsilon\) then stop
If \(x_r-x_m > x_m-x_l\) then do \((a)\) otherwise do \((b)\)
Let \(y=x_m+(x_r-x_m)/(1+\rho)\) if \(f(y) \ge f(x_m)\) then put \(x_l=x_m\) and \(x_m=y\) otherwise put \(x_r=y\)
Let \(y=x_m+(x_m-x_l)/(1+\rho)\) if \(f(y) \ge f(x_m)\) then put \(x_r=x_m\) and \(x_m=y\) otherwise put \(x_l=y\)
Go back to step 1
def gsection(ftn, xl, xm, xr, tol = 1e-9):
# applies the golden-section algorithm to maximise ftn
# we assume that ftn is a function of a single variable
# and that x.l < x.m < x.r and ftn(x.l), ftn(x.r) <= ftn(x.m)
#
# the algorithm iteratively refines x.l, x.r, and x.m and
# terminates when x.r - x.l <= tol, then returns x.m
# golden ratio plus one
gr1 = 1 + (1 + np.sqrt(5))/2
#
# successively refine x.l, x.r, and x.m
fl = ftn(xl)
fr = ftn(xr)
fm = ftn(xm)
while ((xr - xl) > tol):
if ((xr - xm) > (xm - xl)):
y = xm + (xr - xm)/gr1
fy = ftn(y)
if (fy >= fm):
xl = xm
fl = fm
xm = y
fm = fy
else:
xr = y
fr = fy
else:
y = xm - (xm - xl)/gr1
fy = ftn(y)
if (fy >= fm):
xr = xm
fr = fm
xm = y
fm = fy
else:
xl = y
fl = fy
return(xm)
19.2.3. Maximize Function: f¶
We next use these algorithms to find the maximum point of our function f1
and f1simple. Note that if we use the Newton algorithm we will need the
first and second derivatives of the functions. This is why we use function
f1 that returns f, f' and f'' via an array/vector as return value.
print(" -----------------------------------")
print(" Newton results ")
print(" -----------------------------------")
print(newton(f1, 0.25))
print(newton(f1, 0.5))
print(newton(f1, 0.75))
print(newton(f1, 1.75))
-----------------------------------
Newton results
-----------------------------------
-1.25
1.0
0.9999999999980214
14.42367881581733
The Golden section algorithm does not require the derivates of the function, so
we just call the f1simple function that only returns the functional value.
print(" -----------------------------------")
print(" Golden section results ")
print(" -----------------------------------")
myOpt = gsection(f1simple, 0.1, 0.25, 1.3)
print(gsection(f1simple, 0.1, 0.25, 1.3))
print(gsection(f1simple, 0.25, 0.5, 1.7))
print(gsection(f1simple, 0.6, 0.75, 1.8))
print(gsection(f1simple, 0.0, 2.75, 5.0))
-----------------------------------
Golden section results
-----------------------------------
1.0000000117853984
1.0000000107340477
0.9999999921384167
1.0000000052246139
Finally, we can also use a built in function minimizer.
The built in function fmin is in the scipy.optimize library. We need to
import it first. So if we want to maximize our function we have to define it
as a negated function, that is:
then
is the same as
Since we want to find the maximum of the function, we need to “trick” the minimization algorithm. We therefore need to redefine the function as
def f1simpleNeg(x):
# gamma(2,3) density
if (x < 0):
return (0)
if (x == 0):
return (np.nan)
y = np.exp(-2*x)
return (-(4 * x**2 * y))
Here we simply return negative values of this function. If we now minimize this function, we actually maximize the original function
from scipy.optimize import fmin
print(" -----------------------------------")
print(" fmin results ")
print(" -----------------------------------")
print(fmin(f1simpleNeg, 0.25))
print(fmin(f1simpleNeg, 0.5))
print(fmin(f1simpleNeg, 0.75))
print(fmin(f1simpleNeg, 1.75))
-----------------------------------
fmin results
-----------------------------------
Optimization terminated successfully.
Current function value: -0.541341
Iterations: 18
Function evaluations: 36
[1.]
Optimization terminated successfully.
Current function value: -0.541341
Iterations: 16
Function evaluations: 32
[1.]
Optimization terminated successfully.
Current function value: -0.541341
Iterations: 14
Function evaluations: 28
[0.99997559]
Optimization terminated successfully.
Current function value: -0.541341
Iterations: 16
Function evaluations: 32
[1.00001221]
19.3. Finding the Root of a Function using Minimization¶
In a previous chapter on root searching of a function we used various methods like the built in fsolve or root functions from the scipy.optimize library. Here’s the example from the Root finding chapter again:
The example function for which we calculate the root, i.e., find \(x\) so that \(f(x) = 0\) is defined as:
def func(x):
s = np.log(x) - np.exp(-x) # function: f(x)
return s
We can solve for the zero (root) position with:
from scipy.optimize import root
guess = 2
result = root(func, guess) # starting from x = 2
print(" ")
print(" -------------- Root ------------")
myroot = result.x # Grab number from result dictionary
print("The root of d_func is at {}".format(myroot))
print("The max value of the function is {}".format(myOpt))
-------------- Root ------------
The root of d_func is at [1.30979959]
The max value of the function is 1.0000000117853984
In this section we set up the root finding problem as an optimization problem. In order to do this we change the return value of the function slightly to
So we are trying to find the value of
x so that the residual error between \(f(x)\) and its target value of
\(0\) is as small as possible. The new function is defined as:
def func_root_min(x):
s = np.log(x) - np.exp(-x) # function: f(x)
return (s**2)
We now invoke a minimizing algorithm to find this value of \(x\)
from scipy.optimize import minimize
guess = 2 # starting guess x = 2
result = minimize(func_root_min, guess, method='Nelder-Mead')
print(" ")
print("-------------- Root ------------")
myroot = result.x # Grab number from result dictionary
print("The root of func is at {}".format(myroot))
-------------- Root ------------
The root of func is at [1.30976562]
19.4. Multivariate Optimization¶
19.4.1. Function¶
Here we want to optimize the following function f3
def f3simple(x):
a = x[0]**2/2.0 - x[1]**2/4.0
b = 2*x[0] - np.exp(x[1])
f = np.sin(a)*np.cos(b)
return(f)
Its negative version:
def f3simpleNeg(x):
a = x[0]**2/2.0 - x[1]**2/4.0
b = 2*x[0] - np.exp(x[1])
f = -np.sin(a)*np.cos(b)
return(f)
And the version that returns \(f(x)\), \(f'(x)\) (i.e., the gradient), and \(f''(x)\) (i.e., the Hessian matrix):
def f3(x):
a = x[0]**2/2.0 - x[1]**2/4.0
b = 2*x[0] - np.exp(x[1])
f = np.sin(a)*np.cos(b)
f1 = np.cos(a)*np.cos(b)*x[0] - np.sin(a)*np.sin(b)*2
f2 = -np.cos(a)*np.cos(b)*x[1]/2 + np.sin(a)*np.sin(b)*np.exp(x[1])
f11 = -np.sin(a)*np.cos(b)*(4 + x[0]**2) + np.cos(a)*np.cos(b) \
- np.cos(a)*np.sin(b)*4*x[0]
f12 = np.sin(a)*np.cos(b)*(x[0]*x[1]/2.0 + 2*np.exp(x[1])) \
+ np.cos(a)*np.sin(b)*(x[0]*np.exp(x[1]) + x[1])
f22 = -np.sin(a)*np.cos(b)*(x[1]**2/4.0 + np.exp(2*x[1])) \
- np.cos(a)*np.cos(b)/2.0 - np.cos(a)*np.sin(b)*x[1]*np.exp(x[1]) \
+ np.sin(a)*np.sin(b)*np.exp(x[1])
# Function f3 returns: f(x), f'(x), and f''(x)
return (f, np.array([f1, f2]), np.array([[f11, f12], [f12, f22]]))
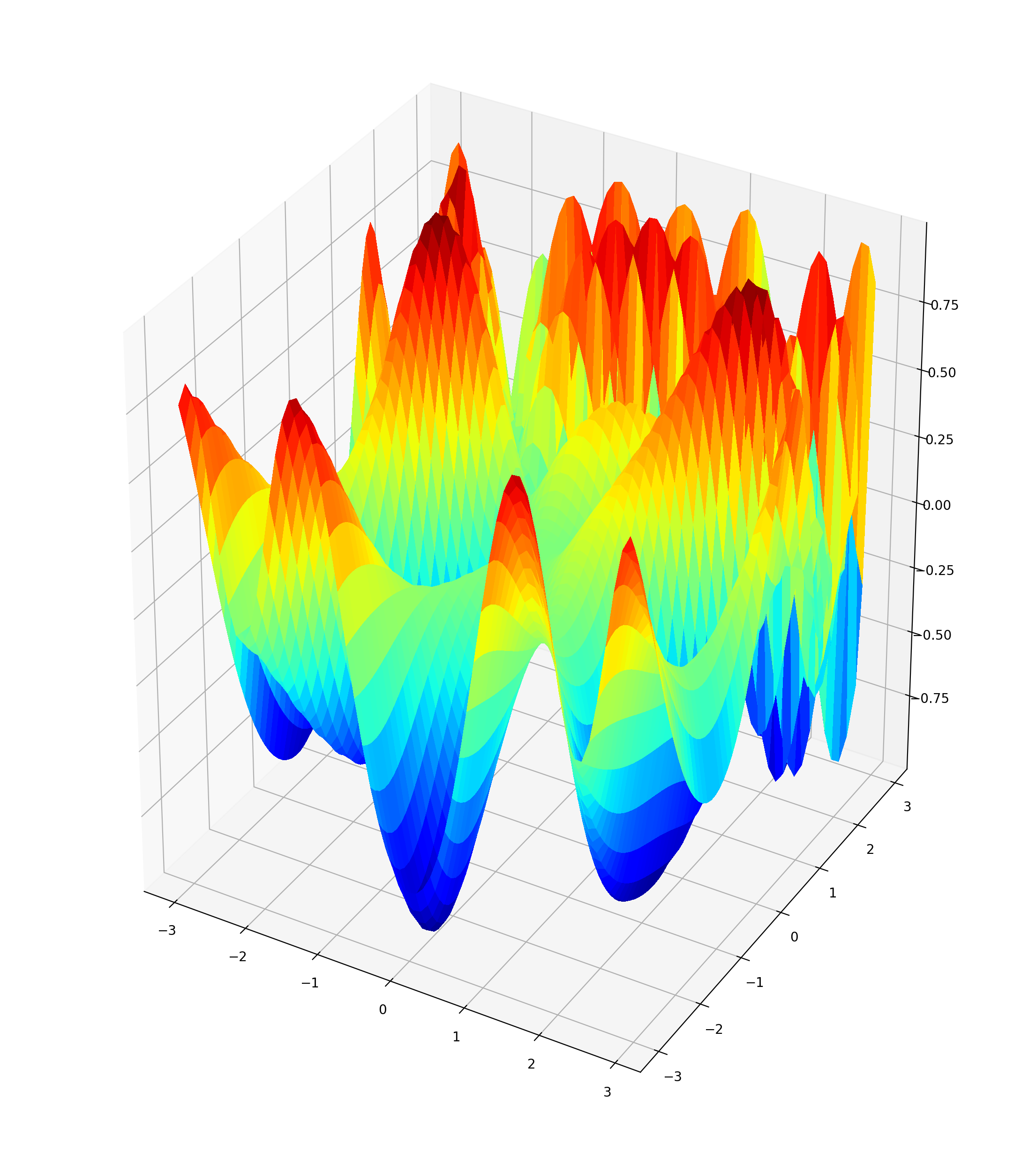
We next plot the function:
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(14, 16))
ax = plt.gca(projection='3d')
X = np.arange(-3, 3, .1)
Y = np.arange(-3, 3, .1)
X, Y = np.meshgrid(X, Y)
Z = np.zeros((len(X),len(Y)),float)
for i in range(len(X)):
for j in range(len(Y)):
Z[i][j] = f3simple([X[i][j],Y[i][j]])
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, \
cmap=plt.cm.jet, linewidth=0, antialiased=False)
plt.show()
19.4.2. Multivariate Newton Method¶
def newtonMult(f3, x0, tol = 1e-9, nmax = 100):
# Newton's method for optimisation, starting at x0
# f3 is a function that given x returns the list
# {f(x), grad f(x), Hessian f(x)}, for some f
x = x0
f3x = f3(x)
n = 0
while ((max(abs(f3x[1])) > tol) and (n < nmax)):
x = x - np.linalg.solve(f3x[2], f3x[1])
f3x = f3(x)
n = n + 1
if (n == nmax):
print("newton failed to converge")
else:
return(x)
Compare the Newton method with the built in fmin method in
scipy.optimize. We use various starting values to see whether we can find
more than one optimum.
from scipy.optimize import fmin
for x0 in np.arange(1.4, 1.6, 0.1):
for y0 in np.arange(0.4, 0.7, 0.1):
# This algorithm requires f(x), f'(x), and f''(x)
print("Newton: f3 " + str([x0,y0]) + ' --> ' + str(newtonMult(f3, \
np. array([x0,y0]))))
print("fmin: f3 " + str([x0,y0]) + ' --> ' \
+ str(fmin(f3simpleNeg, np.array([x0,y0]))))
print(" ----------------------------------------- ")
Newton: f3 [1.4, 0.4] --> [ 0.04074437 -2.50729047]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 47
Function evaluations: 89
fmin: f3 [1.4, 0.4] --> [2.0307334 1.40155445]
-----------------------------------------
Newton: f3 [1.4, 0.5] --> [0.11797341 3.34466147]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 50
Function evaluations: 93
fmin: f3 [1.4, 0.5] --> [2.03072555 1.40154756]
-----------------------------------------
Newton: f3 [1.4, 0.6] --> [-1.5531627 6.0200129]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 43
Function evaluations: 82
fmin: f3 [1.4, 0.6] --> [2.03068816 1.40151998]
-----------------------------------------
Newton: f3 [1.5, 0.4] --> [2.83714224 5.35398196]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 48
Function evaluations: 90
fmin: f3 [1.5, 0.4] --> [2.03067611 1.40149298]
-----------------------------------------
Newton: f3 [1.5, 0.5] --> [ 0.04074437 -2.50729047]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 42
Function evaluations: 82
fmin: f3 [1.5, 0.5] --> [2.03071509 1.40155165]
-----------------------------------------
Newton: f3 [1.5, 0.6] --> [9.89908350e-10 1.36639196e-09]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 43
Function evaluations: 82
fmin: f3 [1.5, 0.6] --> [2.0307244 1.40153761]
-----------------------------------------
Newton: f3 [1.6, 0.4] --> [-0.55841026 -0.78971136]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 47
Function evaluations: 88
fmin: f3 [1.6, 0.4] --> [2.0307159 1.40150964]
-----------------------------------------
Newton: f3 [1.6, 0.5] --> [-0.29022131 -0.23047994]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 44
Function evaluations: 80
fmin: f3 [1.6, 0.5] --> [2.03074135 1.40151521]
-----------------------------------------
Newton: f3 [1.6, 0.6] --> [-1.55294692 -3.33263763]
Optimization terminated successfully.
Current function value: -1.000000
Iterations: 42
Function evaluations: 80
fmin: f3 [1.6, 0.6] --> [2.03069759 1.40155333]
-----------------------------------------