14 Investments and Financial Markets
The theory of investment that says that current investment spending depends positively on the expected future growth of real GDP. Investment is defined as costs today for benefits in the future. The return to investments is usually measured through an interest rate. We distinguish between two rates:
- Nominal interest rates, are the rates charged in the market
- Real interest rates, are nominal rates adjusted for inflation
Financial intermediaries facilitate borrowing and lending between parties that have funds (savers) and parties that are looking for funds to start projects (investors). Financial intermediaries
Receive funds from savers and Channel them to investors.
14.1 Investment and Uncertainty
Investment projects are uncertain, since they involve future and therefore uncertain payoffs. Investments are pro-cyclical, that is they are positively correlated with GDP and they are more volatile than GDP. The multiplier-accelerator theory provides an explanation for this empirical fact.
14.1.1 Accelerator Theory
The Accelerator Theory of investments states that
- Current investment spending depends positively on the expected future growth of real GDP. So if investors feel good about the future state of the economy, they are more likely to invest their funds into projects that start paying off in the future (when the economy is supposedly doing well).
- Investment spending is therefore highly pro-cyclical and more volatile than GDP.
Investment: A Plunge into the Unknown
- The accelerator theory emphasizes the role of expected growth in real GDP on investment spending
Example
- When real GDP growth is expected to be high, firms anticipate that their investments in plant and equipment will be profitable.
- Therefore they increase their total investment spending.
- This becomes a self-fulfilling prophecy as high investments today, will lead to a build up of projects, more hiring so that the economy grows.
In his multiplier-accelerator theory, Nobel laureate Paul Samuelson explained
– how a downturn in real GDP leads to a
– sharp fall in investment, which further
– reduces GDP through the multiplier for investment spending.
In this case the story works in the other direction. An expected future downturn of the economy, leads to investors decreasing their investments, since they expect that the payoffs will be small as the economic environment deteriorates. This also becomes a self-fulfilling prophecy. If investors think that the future will be bad, then their current actions (i.e., decreases in investments) will contribute to the expected downturn.
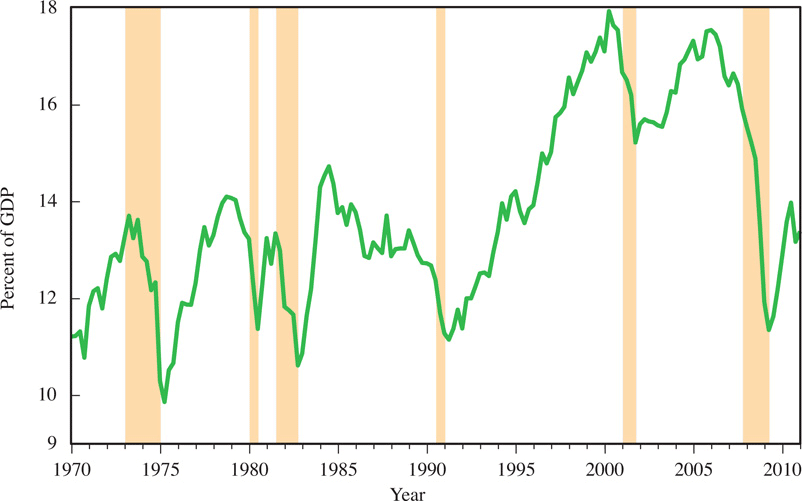
Swings in investment have occurred over short periods of time. During recessions (noted by the shaded areas), investment spending fell sharply.
During booms, investment spending rose sharply. This means that investment spending is highly pro-cyclical. In other words, private investment is positively correlated with GDP.
14.1.2 Evaluating the Future
A dollar paid today is not the same as a dollar paid next year. Think about the following thought experiment. In a year from now you will need $100 dollars to make a specific purchase. Your rich uncle will give you the money but offers you two options: A) Receive $100 today, or B) Receive $100 a year from now.
Which option is better? Keep in mind, you do not need the money right now.
The answer is that before you compare the two options you first need to translate the dollar values in a common unit. A dollar today is not the same thing as a dollar next year. Why is that?
Let's demonstrate this and assume that currently the market interest that a bank offers for deposits is 4%. If you go with option A above and receive the $100 dollars today, then you could put those $100 into your bank account where it will earn 4%. So in a year from now you will have $104 dollars. Had you gone with option B above, you would only have $100 a year from now. So, option A is clearly worth more. In tomorrows dollars, option A is worth $104 compared to option B which is only worth $100 dollars in 'tomorrows dollars'. We have thus translated option A into the same unit as option B and we can now compare its value.
Similarly you could have expressed both options, A and B, in 'today's dollars'. Option A is worth $100 in todays dollars whereas option B is only worth \(\$100/(1+0.04) = \$96.15\). Why is that. Well, if your uncle gives you $96.15 dollars today, then you can put that amount into the bank where it will grow to $96.15 (1+0.04) = \(100\) dollars next year (i.e., tomorrow)
- If we express dollar values in today's dollars, we refer to the values as the present value.
- The process of translating future dollar payments into their present value is called discounting.
When we divided the $100 payment a year from in option B above with one plus the market interest rate, we discounted the future value back into today's value.
A different way of thinking about this is as follows. The present value of a payment to be received in the future is the maximum amount a person is willing to pay today to get that payment later.
As the interest rate increases, the opportunity cost of your funds also increases, so the present value of a given payment in the future falls. This means that you need less money today to get to your future “money goal”.
Present Value and Interest Rates
Present value definition:
\[PV=\frac{K}{\left(1+i\right)^{t}}\]
- K= amount of money you would get at some point in the future
- t=amount of time, or years, in the future you’re going to get the money
- i=interest rate you are going to earn
The present value of a given payment in the future decreases as the interest rate increases. When interest rates fall, the present value of a given payment in the future increases.
Example 1
Future payment one year from now:
\[K=\$400, t=1, i=3\%\]
Present value definition:
\[PV=\frac{400}{\left(1+0.03\right)^{1}}=388.35\]
Example 2
Future payment two years from now:
\[K=\$400, t=2, i=3\% \text{ for both years}\]
Present value definition:
\[PV=\frac{400}{\left(1+0.03\right)^{2}}=377.04\]
Example 3
Two future payments: $400 one year from now and $450 two years from now
\[t=2, i=3\% \text{ for both years }\]
Present value definition:
\[PV=\frac{400}{\left(1+0.03\right)}+\frac{450}{\left(1+0.03\right)^{2}}=812.52\]
Example 4
Future payment two years from now:
\[K=\$400, t=2, i_{1}=3\% \text{ in year one and } i_{2}=5\% \text{ in year two}\]
Present value definition:
\[PV=\frac{400}{\left(1+0.03\right)\times\left(1+0.05\right)}=369.86\]
Example 5
- Two future payments: $400 one year from now and $450 two years from now
- \(i_{1}=3\%\) in year one and \(i_{2}=5\%\) in year two
Present value definition:
\[PV=\frac{400}{\left(1+0.03\right)}+\frac{450}{\left(1+0.03\right)\times\left(1+0.05\right)}=804.44\]
Example 6
- Investment project with initial setup cost of: $600
- Two future payments: $400 one year from now and $450 two years from now
- \(i_{1}=3\%\) in year one and \(i_{2}=5\%\) in year two
Present value definition:
\[NPV=-600+\overset{PV}{\overbrace{\frac{400}{\left(1+0.03\right)}+\frac{450}{\left(1+0.03\right)\times\left(1+0.05\right)}}}=204.44\]
This is often referred to as the net-present value (NPV)
Investment rule: if \(NPV > 0 \rightarrow\) make investment!
14.1.3 Real and Nominal Interest Rates
Calculating the true cost of borrowing or lending involves the reality principle:
Real-Nominal PRINCIPLE
What matters to people is the real value of money or income—its purchasing power—not the “face” value of money or income
When there is inflation, economists make a distinction between the interest rate quoted in the market, i.e., the nominal interest rate, and the real interest rate which measures what an investor/household actually earns after inflation has been taken into account.
- Real rate = Nominal rate – Inflation rate
Nominal and Real Interest Rates
A bond is a promise or IOU to pay money in the future in exchange for money now
Money is paid back including an interest payment
- Real interest rate: r
- Nominal interest rate: i
- Inflation rate:\(\pi\), so that
\[r=i-\pi\]
14.1.4 Expected Inflation
When individuals borrow or lend, they do not know what the rate of inflation, \(\pi\) will be. Hence they need to form expectations, \(\pi^{e}\) and then base their decisions upon those. So an investor who thinks about an investment with future payoff will operate with an
- Expected real interest rate: \(r^{e}=i-\pi^{e}\)
when evaluating investment projects.
The expected real interest rate is the rate at which borrowers or lenders expect to make transactions in the future.
Bonds are debt contracts or I.O.U.s (I owe you). A bond is a piece of paper issues by a government (government or treasury bond), a firm (corporate bond) or a private person (I.O.U debt contract) that states the amount owed at a certain time in the future.
Corporate bonds are considered more risky than federal government bonds, so they have to pay a higher interest rate in order to compensate investors for the additional risk.
- The value of corporate bonds, depends on the well being of the corporation that issues the debt contract. If a firm goes out of business, its debt contracts might not be served, so that investors in bonds of this company will then lose all or parts of their money.
- The value of a government bond depends on the underlying value of the entire economy that the government represents. It is less likely that an entire country declares bankruptcy. So overall, corporate bonds, or debt contracts, are therefore more risky.
- Long term investments are more risky than short term investments, so they pay a higher interest rate.
- Nominal interest rate
- Real interest rate
- Bonds and rates of return
- What does it mean when we say investment is pro-cyclical?
- Why is the distinction between nominal and real interest rates important?
14.2 Investment Spending and Interest Rates
Interest rate provides a measure of opportunity cost for investments. If you do not invest your money into a private investment project, you can always put it into the bank where it earns the market interest rate. So the opportunity cost of investing in the private sector is the forgone interest rate.
14.2.1 Investment Spending and Interest Rates
Now that we understand the concept of present value and interest rates, we can use these tools to understand investment decisions. Consider a project we have to pay for today in order to benefit in the future. Only if the investment projects promises to pay a higher rent than the prevailing market interest rate, would it be profitable to invest.
Investment Rule:
Investment Rule Invest in a project if the cost you incur today is less than or equal to the present value of the future payments from the project.
Here is a brief example. You have the opportunity to invest in a number of different investment projects. Their initial cost and their payoff at the end of the year is depicted in the following table.
| Project | Cost | Return |
|---|---|---|
| A | $100 | $101 |
| B | $100 | $103 |
| C | $100 | $105 |
| D | $100 | $107 |
| E | $100 | $109 |
Let us assume that the current market interest rate is 2% per year. If that is the case then only investment A is unprofitable. All other projects earn a return higher than the market interest rate, that is return greater than the opportunity cost of the funds.
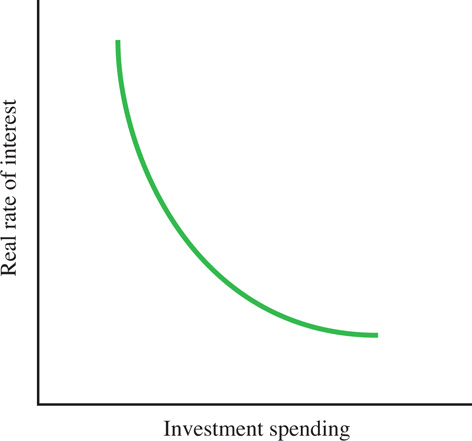
As you can see from Figure 14.3, as the market interest rate rises, there will be fewer profitable investments. Hence, the total level of investment will decline as real interest increases
In practice, firms need to take into account other factors besides interest rates in making their investment decisions. In the neoclassical theory of investment, pioneered by Dale Jorgenson of Harvard University, taxes along with real interest rates play a key role in determining investment spending. Jorgenson used his theory to analyze how investors respond to a variety of tax incentives, including investment tax credits.
Should we use a real or nominal interest rate to determine whether to invest? The answer is that it doesn’t really matter, as long as we are consistent. If the future benefits of the project are not adjusted for inflation, then we should use the nominal interest rate because it takes into account overall inflation. That is, inflation is built into the nominal rate, so to speak. But if we first express the future benefits of the investment in current dollars—that is, if we reduce their nominal value by the amount that prices in the economy are expected to increase—then we should use the real rate of interest in our calculations.
I recommend you stick with real interest rates and discounted future cash flows as a rule.
Keep this distinction between real and nominal interest rates in mind. If nominal interest rates are 10 percent but inflation is 9 percent, the real rate of interest is only 1 percent. A firm makes its investment decisions by comparing its expected real net return from investment projects to the real rate of interest. Just because nominal interest rates are high does not mean the real interest rate is also high. During the 1970s, homeowners in California understood this. They purchased homes in record numbers, even though it meant borrowing money at interest rates exceeding 10 percent. Buyers were willing to borrow at such high rates because housing prices in California had been rising by more than 10 percent annually, and they believed the trend would continue. They realized, for example, that if housing prices rose by 12 percent per year, they were essentially earning a 2 percent annual return because their mortgage loans were just 10 percent. (They would earn the returns only when they sold their homes.) That would make the real interest rate of the money borrowed -2 percent. This caused a housing boom in California that lasted until housing prices stopped rising at such high rates.
High Interest Rates and High Investment?
It is possible to observe high interest rates and high investment levels at the same time. How is this possible? Didn't we just describe an inverse or negative relationship between the market interest rate and the level of investment?
If the nominal interest is high and the inflation rate is high as well, then the real interest might actually be low. If real interest is low, then investment is high. It is the real interest rate that ultimately determines the level of investment. If it is low, then the investment level is high.
14.2.2 Investment Theories
So far we have talked about the role of interest rates in determining investment levels in the economy.
Neoclassical theory of investment
The neoclassial theory of investment states that real interest and taxes are the major factors determining investment (Dale Jorgenson of Harvard University)
In addition, economists have long noticed a correlation between the stock market and investment spending. All other things being equal, when the level of the stock market is high, investment spending also tends to be high. It makes sense that the two are related. Consider a firm’s options when it wants to finance a new project. The firm really has three choices:
- First, it can rely on its retained earnings—the earnings the firm hasn’t paid out in dividends to its owners.
- Second, it can borrow funds from a bank or sell corporate bonds to the public.
- Third, it can issue and sell new shares, or stock.
When a firm’s stock price is high, it can issue shares at a premium and use the proceeds from their sale to finance new investments. The higher the share price, the fewer shares the firm needs to sell to raise capital. This means, essentially, that the cost of the project the firm wants to undertake falls as the company’s stock price climbs. In other words, high stock prices lead to high investment. This is known as the Q-theory of investment, and it was originally developed by the late Nobel Laureate James Tobin of Yale University. In the boom of the late 1990s when the level of the stock market was high along with share prices, many firms financed large investments by selling their shares.
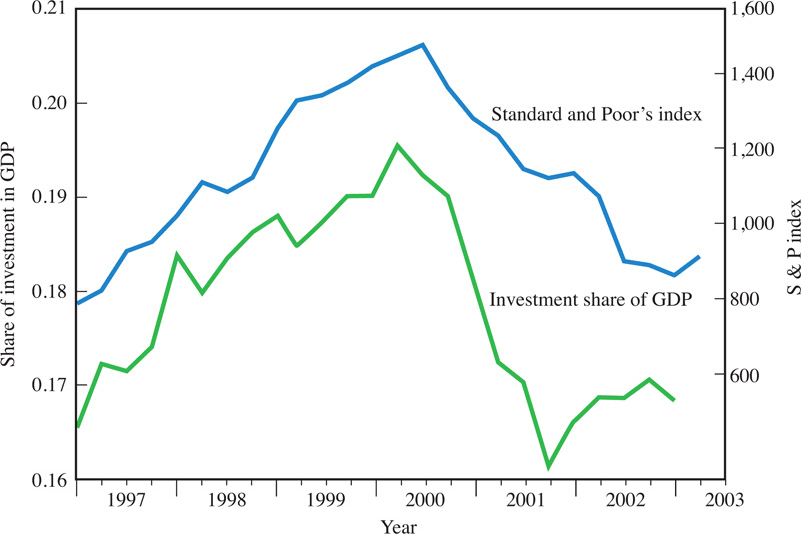
During roughly this same time period, the stock market and investment spending appeared to be even more tightly linked than in the past. Figure 12.4 plots the Standard and Poor’s index of stock prices on the same graph as the share of investment spending as a component of GDP from 1990 to 2013. Looking at a historical example, both the stock market and investment spending rose sharply from 1997, peaking in mid-2000.
They then both fell sharply—the stock market plunged, investment spending fell, and the economy entered a recession. This is a typical pattern as you can see in Figure 14.4.
The reason the two were so tightly linked in 1997–2000 was that investors were overly optimistic about the future. They believed that, driven by new technology, the newfound economic prosperity would last forever (or at least certainly longer than it did). With optimistic expectations about the future, stock prices should have been high because stock prices are based on the present value of the dividends people expect firms to pay in the future:
Stock prices are based on the present value of the dividends people expect firms to pay in the future. The price of a stock is the present value of future discounted dividend payments:
\[p_{stock}=\frac{d_{1}}{\left(1+i\right)^{1}}+\frac{d_{2}}{\left(1+i\right)^{2}}+\frac{d_{3}}{\left(1+i\right)^{3}}+...\]
Because investors’ expectations about future dividends were high, stock prices were high. Firms, like individual investors, rushed to make massive, long-term investments, particularly in the fiber-optics and telecommunications industries. Some observers questioned whether the expectations were rational. Still, there were enough optimistic investors to sufficiently drive up prices. In many cases, stock prices for companies that had never turned a profit nonetheless soared to astronomical heights.
Unfortunately, both investors and firms may have been subject to what former Federal Reserve chairman Alan Greenspan famously dubbed “irrational exuberance”— something similar to Keynes’s “animal spirits.” Although the economy had performed very well in the late 1990s, it could not grow at those rates forever. Many investors and firms believed it could, though. When they began to realize it couldn’t, the stock market plunged and investment plans were curtailed. What linked the stock market and investment in both their rise and their fall were first optimistic and then pessimistic expectations about the economy. Rather than causing the rise and fall of investment spending, the stock market mirrored expectations about the economy held by firms and individual investors.
The Q-theory of investment, developed by Nobel laureate James Tobin of Yale University, links investment spending to stock prices. It states that investment spending increases when stock prices are high. Then, the firm uses its proceeds from the sale of stocks to undertake new investment.
Q-Theory of investment
- The Q-Theory of investment states that stock market prices are one of the major factors in determining the level of investment.
There is an inverse relationship between real interest rates and the level of private investment as the interest rate is the opportunity cost of investment.
The neoclassial theory of investment states that real interest and taxes are the major factors determining investment (Dale Jorgenson of Harvard University)
The Q-Theory of investment states that stock market prices are one of the major factors in determining the level of investment.
- If the central bank raises the interest rate, what happens to private investment?
14.3 Financial Intermediaries
Households save and invest their funds for different reasons than firms. A typical couple might be saving money for their retirement or for their children’s education, and they generally won’t like the idea of their savings being subject to risk. They do, however, want their savings to be readily accessible and convertible to money—what economists call liquid—in case they have a financial emergency. Funds deposited in a bank account, for example, provide a source of liquidity for households because they can be withdrawn at any time.
Unlike households, firms and business managers are typically risk-takers. They are gambling that their vision of the future will come true and make them vast profits. These investors need funds they can tie up for long periods of time. For example, an entrepreneur who wants to build a skyscraper or casino may need financing for several years before beginning construction and for years afterward until the business begins to produce profits.
Suppose individual entrepreneurs had to obtain funds directly from individual savers. First, they would have to negotiate with thousands of people to obtain sufficient funds. This would take a lot of time and be costly. Second, the savers would face extraordinarily high risks if they loaned all their money to a single entrepreneur who had a risky project to undertake. Not only would all their funds be tied up in a single project, it would not be easy to monitor the investor’s decisions. How could they be certain the entrepreneur wouldn't run off with their money? Additionally, their investments would not be liquid. To compensate these savers for the risk they would be taking and the lack of liquidity they would face, entrepreneurs would have to pay them extremely high interest rates, but higher interest rates would make it harder, perhaps impossible, for the entrepreneur to make a profit. No prospect of profits would mean no one would invest in the project in the first place. In other words, society would not be able to turn its savings into profitable investment projects. Figure 12.5 depicts this dilemma. How can the problem be solved?
The answer is through financial intermediaries. Financial intermediaries include banks, savings and loans, insurance companies, brokerage firms, companies that run mutual funds, and other types of financial institutions. These institutions accept funds from savers and make loans to businesses and individuals. For example, a local bank accepts deposits from savers and uses the funds to make loans to local businesses. Savings and loan institutions will accept deposits in savings accounts and use these funds to make loans, often for housing. Insurance companies accept premium payments from individuals in exchange for the protection provided by the insurance payments. Then insurance companies lend the premiums received to earn returns from investments so they can pay off the insurance claims of individuals. Figure 12.6 shows how financial intermediaries create a valuable link between savers and investors. Pooling the funds of savers to make loans to individual borrowers reduces the costs of negotiation. Financial institutions also have more expertise to evaluate and monitor investments than most individual investors.
To some degree, these financial intermediaries also provide liquidity. In normal circumstances, not all households withdraw their money at the same time, so financial intermediaries can lend out most of the money and still have enough on hand to meet withdrawals by depositors.
But how do financial intermediaries reduce risk? They do this by diversifying investors’ assets—by not putting “all the eggs in one basket,” so to speak. Intermediaries invest (that is, make loans) in a large number of projects whose returns, although uncertain, are independent of one another. By independent, we mean the return from one investment is unrelated to the return on another investment. Consider a bank investing in a large number of projects that all together produce an average return of 8 percent annually. Each project alone is risky and could pay a return either higher or lower than 8 percent. However, as long as the returns on all these projects are independent of one another, those with higher returns will likely offset those with lower returns. By investing in a large number of projects, the bank increases the odds that as a group the projects will earn 8 percent.
Other financial intermediaries reduce risks in related ways. A fire insurance company accepts premiums from many individuals in communities throughout the country and uses the funds to make investments. Because not all houses will burn down in the same year, the insurance company knows it will have a stable source of funds for its investments. Insurance diversification works well only when companies insure events that are independent of one another, however. Some situations are not independent and therefore can’t easily be insured by the same company. For example, an insurance company would be unwise to provide earthquake insurance for just the Los Angeles area. If an earthquake did occur, the firm would be faced with making payments to many clients who suffered loss without anyone else’s payments to offset them. In somewhat the same way, even bank loans are not fully independent. During a recession, many more firms will experience financial difficulties and have trouble meeting their loan obligations to their banks.
In recent years, we have seen an innovation in financial intermediation. In the past, if a savings and loan company made a loan to a home purchaser, it would hold onto the loan until it was paid off. That meant the savings and loan could make new loans or mortgages only if it was able to attract new deposits to provide the funds. Two large government-sponsored financial intermediaries, Fannie Mae and Freddie Mac, changed the way mortgage markets operated. They purchased mortgages from savings and loans and banks throughout the country, packaged them, and sold them to investors in the financial market. This enabled savings and loans to offer additional mortgages with the funds they received from Fannie Mae or Freddie Mac, and it allowed investors to own a part of a diversified collection of mortgages from around the country. The private sector quickly adopted these practices as well.
The practice of purchasing loans, repackaging them, and selling them to the financial markets is known as securitization. Although it started with home mortgages, securitization now applies to other types of financial obligations, such as credit card and consumer debt. Financial intermediaries will often borrow money from financial markets to purchase loans in order to repackage and sell them. Using borrowed funds to purchase assets is known as leverage. Increases in leverage increase the risk that financial intermediaries undertake because they are obligated to pay off the funds they have borrowed, regardless of the actual performance of the assets they have purchased.
Some Terms
- Securitization
-
The practice of purchasing loans, re-packaging them, and selling them to the financial markets
- Leverage
-
Using borrowed funds to purchase assets
Without intermediaries entrepreneurs would have to borrow directly from households. HH are risk averse and want ready access to their funds. HH would ask very high interest rates to compensate them for the risk. At very high interest rates, only very few investment projects could be realized. Economic growth would be very slow.
Financial intermediaries (i.e., Banks and financial institutions) pool assets and lend at a larger scale. This reduces the cost of borrowing and lending and makes investing at a higher level possible.
In addition, financial intermediaries:
- Monitor investments - Reduce risks via diversification - Provide liquidityFinancial intermediaries help bring savers and investors together. By using their expertise and the powers of diversification, financial intermediaries reduce risk to savers and allow investors to obtain funds on better terms.
Why Financial Intermediaries Emerge
- By pooling the funds of savers and making loans to individual businesses, financial intermediaries reduce the costs of negotiation.
- Financial intermediaries also acquire expertise in both evaluating and monitoring investments.
- Some financial intermediaries also provide the liquidity that households demand. In the absence of financial intermediaries households would have to lend directly to investors. In this way a household would have her savings tied up in an investment project. What if the investment project only pays of in say 5 years, but the household requires the funds earlier due to an emergency? The household would not be able to access the funds. When a household lends through an intermediary, the intermediary always provides the necessary liquidity. So if the households needs her savings back, then she will be able to withdraw her savings while investment projects are still being undertaking and financed with savings from other households. The financial intermediary pools the savings of many households and is therefore able to not only provide liquidity but also lower risk as the bank invests in many different investment projects and not just in one.
Financial intermediaries are:
- Banks, - Insurance companies, - Mutual funds etc
- Describe the role of financial intermediaries.
14.4 Financial Innovation and Risk
During the housing boom, many homeowners borrowed money to purchase their property but then saw the value of their homes fall sharply. In 2012 approximately 12 million U.S. homeowners owed more on their home mortgages than their home was actually worth, this is commonly known as being “underwater”.
Reducing Debt Owed on Home Mortgages -----------------------------------
Many in Congress have advocated for reduction on the amount of money they actually owe—or principal reduction. This idea, however, has proven to be extremely controversial for several reasons:
- First, the holders of the mortgage may not want to reduce the principal because they believe they will be eventually repaid
- Second, what about those underwater homeowners who are meeting their mortgage payments? Would they stop making payments in order to obtain some principal relief?
- Rather than actual principal reduction, some lenders have allowed borrowers to postpone payments or make other arrangements
14.4.1 When Financial Intermediaries Malfunction
Financial intermediation can sometimes go wrong. When it does, the economy suffers. Important examples of the failure of financial intermediation include commercial bank failures during the Great Depression, the U.S. savings and loan crisis of the 1980s, a similar crisis in Japan in the 1990s, and the U.S. housing credit and securitization crisis of 2007 and 2008.
In the early days of the Great Depression, many banks in the United States, particularly in rural areas, provided farmers and local businesses with loans that turned out to be unprofitable. This worried depositors, and rumors circulated that banks would fail. Depositors panicked, and many tried to withdraw their money simultaneously in what is called a bank run. During the Great Depression, bank runs occurred throughout the world. In 1931, a panic broke out after the collapse of Creditanstalt, Austria’s largest bank. Banking panics occurred throughout other countries in Europe, including Belgium, France, Germany, Italy, and Poland.
Few banks, profitable or unprofitable, can survive a run because not all deposits are kept on hand. The result of the bank runs was that thousands of healthy U.S. banks shut down, leaving large parts of the United States without a banking system. Many farms and businesses could no longer find a source of loans, and the severity of the Great Depression worsened. Studies have shown that the countries with the most severe banking panics were hardest hit by the Depression.
To prevent banking panics from happening again, in 1933 the U.S. government began providing deposit insurance on money placed in banks and savings and loans. Today deposit insurance guarantees the government will reimburse depositors for amounts up to $250,000 in each account at each bank should their banks fail. Because everyone knows their deposits are secure, bank runs no longer regularly occur. Today, most countries have some form of deposit insurance intended to prevent panics. Ironically, deposit insurance indirectly led to the U.S. savings and loan crisis, which occurred during the 1980s. In the early 1970s, savings and loan institutions (S&Ls) made mortgage loans to households at low interest rates. However, later in the decade nominal interest rates rose sharply as inflation increased. The savings and loans were in trouble: They had to pay high interest rates to attract deposits, but they were earning interest at low rates from the money they had loaned out previously. Many of the S&Ls failed.
The government tried to assist the savings and loan industry by broadening the range of investments the industry could make. Some S&Ls soon began aggressively investing in speculative real estate and other risky projects to earn higher returns. Depositors weren’t worried, though, because they knew their savings were insured by the government. Unfortunately, many of these risky projects failed, and the government was forced to bail out the S&Ls at a cost of nearly $100 billion to taxpayers. Because depositors’ savings were insured, most people didn’t suffer directly from the collapse of their savings and loan institutions. As taxpayers they suffered, though, because they had to foot the bill.
Japan suffered similar problems in the 1990s. By 1995, seven of the eight largest Japanese mortgage lenders had gone bankrupt following a crash in real estate prices. Like the U.S. government, the Japanese government also used taxpayers’ funds to bail these lenders out. The decline in housing prices that we described in the chapter-opening story triggered a severe crisis in the newly developed securitization markets. Although the actual details are complex, the basic story is simple. Lenders had made loans to borrowers who had limited ability to repay, and when borrowers began to miss payments or default on their loans, it caused major disruptions in the market for securitized loans, which, in turn, disrupted credit to other sectors in the economy, causing a massive disruption to financial markets. Even Fannie Mae and Freddie Mac fell victim to the housing decline and were placed under direct government control in September 2008.
As the housing-generated financial crisis spread to the rest of the financial markets, the credit markets essentially “froze” and banks worldwide would no longer lend to each other. Customers scrambled to withdraw their funds in financial institutions that they perceived were weak, leading to a “run” on these institutions. As a result, financial institutions such as Bear Stearns and Lehman Brothers were forced to close and institutions such as Merrill Lynch and Wachovia Bank were taken over by other financial institutions. When the financial institution Lehman Brothers failed, it set off a panic in the markets that spread to other international banks and financial institutions. The stock market plunged dramatically worldwide, reflecting the severity of the crisis and fear that it would lead to a total worldwide financial collapse. As credit became unavailable, businesses began to suffer as well, as they were not able to borrow funds to run their enterprises on a day-to-day basis. State and local government also found it nearly impossible to borrow at the height of the crisis.
Governments around the world took a number of steps to alleviate this crisis. Central banks, whose activities during the crisis are described in more detail in the next chapter, provided loans and credit through a wide variety of channels. After considerable turmoil, the U.S. Congress passed a bailout package, called the Troubled Asset Relief Program, or TARP, that enabled the Treasury to use up to $700 billion to shore up the financial system. Following the lead of Great Britain, the U.S. Treasury used some of these proceeds to provide funds to large banks in order to restore confidence in the financial system and took limited ownership in these banks. As previously noted, the government took control of Fannie Mae and Freddie Mac and also provided funding to some large financial firms, such as the American International Group (AIG), which provided financial insurance to other firms and was deemed essential to keep afloat during the crisis. The United States and other countries around the world also increased the limits on the amounts eligible for deposit insurance to bolster consumer confidence in banking institutions. The U.S. Congress also enacted the Dodd-Frank legislation, which added a new set of regulatory tools. Similar actions were taken by other large governments around the world. The goals of all these actions were to restore confidence in a system of financial intermediation that was under considerable stress.
From these examples you can see why financial intermediation does not always work. There is a continual debate on the role government should play in investment decisions for the economy and its role in regulating financial intermediaries. Today, some economists and policymakers are carefully reassessing the risks in our complex financial markets.
14.4.2 Financial Innovations and New Risks
As securitization developed, it allowed financial intermediaries to provide new funds for borrowers to enter the housing market. As the housing boom began in 2002, lenders and home purchasers began to take increasing risks.
Lenders made “subprime” loans to borrowers with limited ability to actually repay their mortgages. Some households were willing to take on considerable debt because they were confident they could make money in a rising housing market.
Lenders securitized the subprime loans and financial firms offered exotic investment securities to investors based on these loans (bundling of subprime loans to reduce (or hide?) the true risk of these financial assets).
Many financial institutions purchased these securities without really knowing what was inside them. When the housing boom stopped and borrowers stopped making payments on subprime loans, it created panic in the financial market.
Effectively, through securitization the damage from the subprime loans spread to the entire financial market, causing a major crisis.
If homeowners owe more on their home mortgages than their home is actually worth, we refer to this as being “underwater”.
A brief history of financial crises:
Commercial bank failures in 1930
- Unprofitable loans to farmer or local businesses
- Depositors panicked which resulted in bank runs where depositors lined up in front of their bank trying to withdraw their deposits. Many banks were destroyed as they were not able to repay all the deposits all at once.
- As a result, and in order to reduce the risk and prevent future bank runs and banking crises, the government introduced government backed deposit insurance for up to $100,000.
1980 in the U.S. a savings and loan crisis
1990 Financial crisis in Japan
2007/2008 Subprime Mortgage Crisis started in the U.S.
- Describe what caused the most recent financial crisis in the U.S.