# https://github.com/ageron/handson-ml/
import numpy as np
import pandas as pd
import os
import tarfile
from six.moves import urllib15 Machine Learning: A First Example with OLS
15.1 A First Regression Model Example
15.1.1 Downloading the Data
We again start by first importing some libraries.
We first need to download the data from GitHub:
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/"
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL):
tgz_path = os.path.join("housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall()
housing_tgz.close()
fetch_housing_data()Once that is done, we store the data on our local drive. You want to avoid downloading the data each time you run the script file. So download it once, store it and then comment the download section of your code out and just read the data from your local drive using the pd.read_csv() function from the numpy library. We then can use a few commands to look at our data which is organized or stored in a Pandas DataFrame object.
housing = pd.read_csv("Lecture_MachineLearning_1/housing.csv")
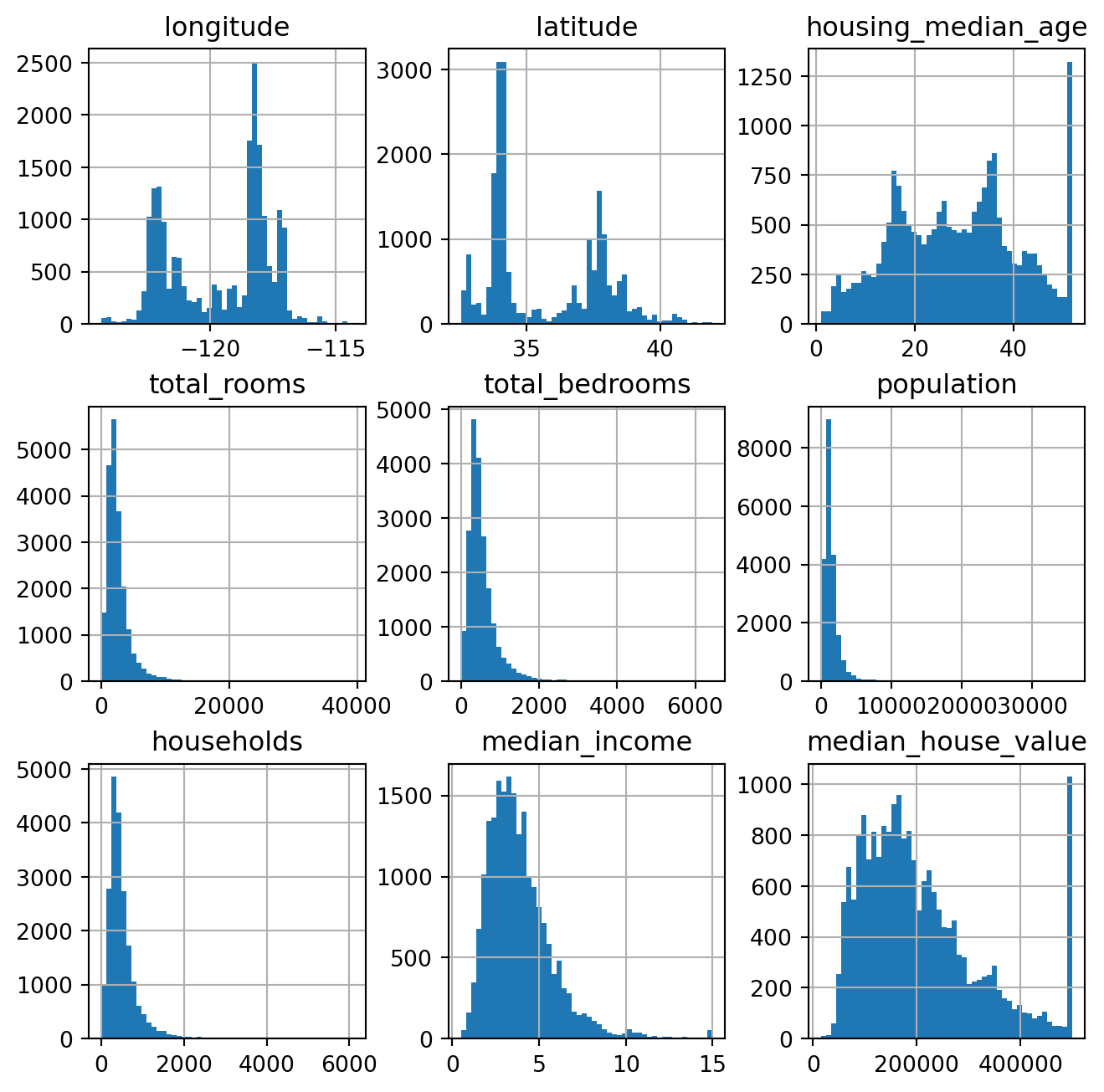
print(housing.head()) longitude latitude housing_median_age total_rooms total_bedrooms \
0 -122.23 37.88 41.0 880.0 129.0
1 -122.22 37.86 21.0 7099.0 1106.0
2 -122.24 37.85 52.0 1467.0 190.0
3 -122.25 37.85 52.0 1274.0 235.0
4 -122.25 37.85 52.0 1627.0 280.0
population households median_income median_house_value ocean_proximity
0 322.0 126.0 8.3252 452600.0 NEAR BAY
1 2401.0 1138.0 8.3014 358500.0 NEAR BAY
2 496.0 177.0 7.2574 352100.0 NEAR BAY
3 558.0 219.0 5.6431 341300.0 NEAR BAY
4 565.0 259.0 3.8462 342200.0 NEAR BAY We can get a quick summary of our data using the .info() function on the dataframe.
print(housing.info())<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 20640 non-null float64
1 latitude 20640 non-null float64
2 housing_median_age 20640 non-null float64
3 total_rooms 20640 non-null float64
4 total_bedrooms 20433 non-null float64
5 population 20640 non-null float64
6 households 20640 non-null float64
7 median_income 20640 non-null float64
8 median_house_value 20640 non-null float64
9 ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
None15.1.2 Inspecting the Data
We can also get some summary statistic for specific feature variables (in econometrics we refer to these as independent variables). We can check the variable ocean_proximity for instance. It is a categorical variable. We cannot do any numerical statistics with this but we can get a feel for this variable by counting how many observation by category we have.
print(housing["ocean_proximity"].value_counts())<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64Finally, we can use the .describe() dataframe method (or function) to get certain summary statistics for each data column.
print(housing.describe()) longitude latitude housing_median_age total_rooms \
count 20640.000000 20640.000000 20640.000000 20640.000000
mean -119.569704 35.631861 28.639486 2635.763081
std 2.003532 2.135952 12.585558 2181.615252
min -124.350000 32.540000 1.000000 2.000000
25% -121.800000 33.930000 18.000000 1447.750000
50% -118.490000 34.260000 29.000000 2127.000000
75% -118.010000 37.710000 37.000000 3148.000000
max -114.310000 41.950000 52.000000 39320.000000
total_bedrooms population households median_income \
count 20433.000000 20640.000000 20640.000000 20640.000000
mean 537.870553 1425.476744 499.539680 3.870671
std 421.385070 1132.462122 382.329753 1.899822
min 1.000000 3.000000 1.000000 0.499900
25% 296.000000 787.000000 280.000000 2.563400
50% 435.000000 1166.000000 409.000000 3.534800
75% 647.000000 1725.000000 605.000000 4.743250
max 6445.000000 35682.000000 6082.000000 15.000100
median_house_value
count 20640.000000
mean 206855.816909
std 115395.615874
min 14999.000000
25% 119600.000000
50% 179700.000000
75% 264725.000000
max 500001.000000 We next start with analyzing our data using graphs and simple statistics.
15.1.3 Splitting the Data
In machine learning it is important to be able to assess how well your trained model can predict outcome variables (or label variables in the case of supervised machine learning). In order to do this we need to split the sample into a training sample that you use to train (estimate) the model with and into a test sample that you can then use to verify how well your model makes out of sample predictions.
It is important that you randomly split the sample and that both samples maintain the features of the overall sample. For instance if your main sample contains 45 percent men, then you want to split the sample in such a way that the training sample has roughly 45 percent men in it and the test sample has roughly 45 percent men in it.
In order to accomplish this we use the built in command train_test_split from the sklearn machine learning library. When you call this function you need to specify how large you want the test sample to be. Below we choose a split that maintains 80 percent of the observations in the raw data for the training sample and 20 percent for test sample. We set the random seed by hand, so that our results become reproducible, i.e., the sample is split in exactly the same way each time we run the script file.
from sklearn.model_selection import train_test_split
# to make this notebook's output identical at every run
np.random.seed(42)
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)We can now inspect the test sample.
print(test_set.head()) longitude latitude housing_median_age total_rooms total_bedrooms \
20046 -119.01 36.06 25.0 1505.0 NaN
3024 -119.46 35.14 30.0 2943.0 NaN
15663 -122.44 37.80 52.0 3830.0 NaN
20484 -118.72 34.28 17.0 3051.0 NaN
9814 -121.93 36.62 34.0 2351.0 NaN
population households median_income median_house_value \
20046 1392.0 359.0 1.6812 47700.0
3024 1565.0 584.0 2.5313 45800.0
15663 1310.0 963.0 3.4801 500001.0
20484 1705.0 495.0 5.7376 218600.0
9814 1063.0 428.0 3.7250 278000.0
ocean_proximity
20046 INLAND
3024 INLAND
15663 NEAR BAY
20484 <1H OCEAN
9814 NEAR OCEAN One thing that is important when splitting the data is to maintain the composition of the data in the subsamples, so that subsamples correctly represent the large sample. Let us look at an example.
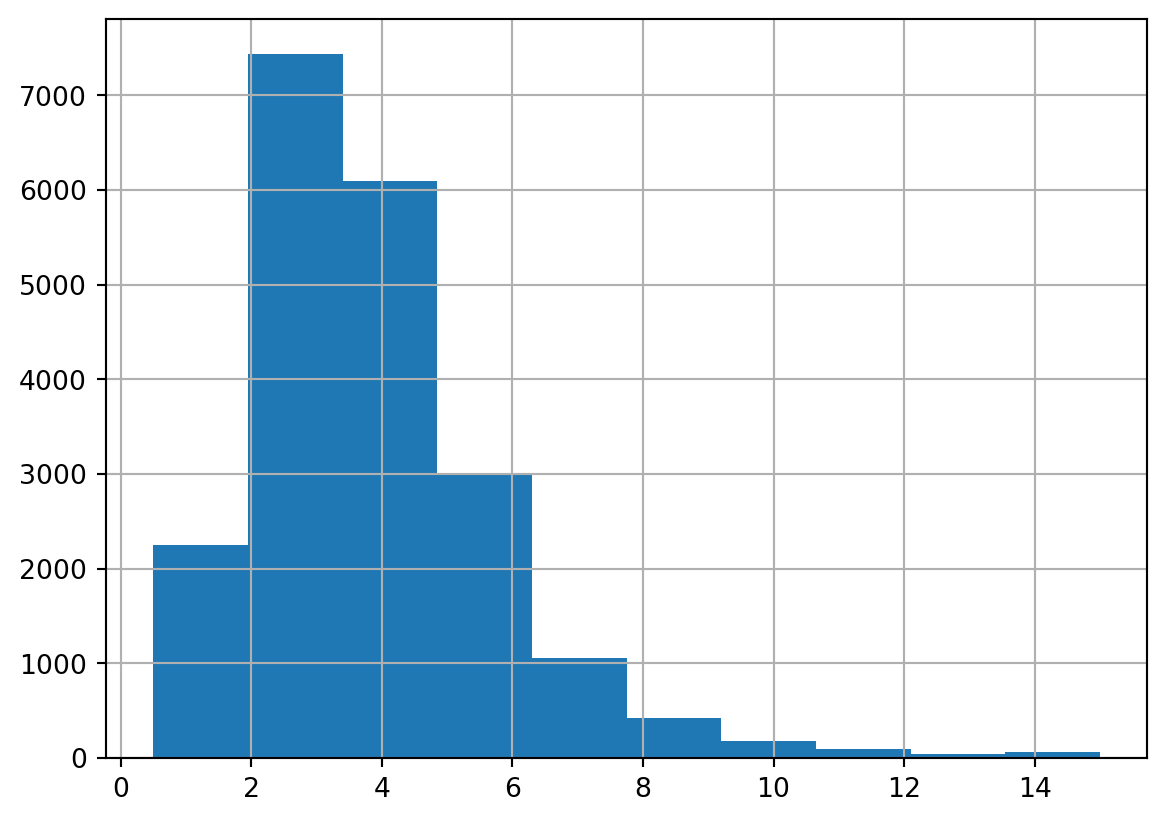
If we analyze income using the histogram plot we have the following distribution of income.
We can also make a categorical variable out of income using the following command.
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
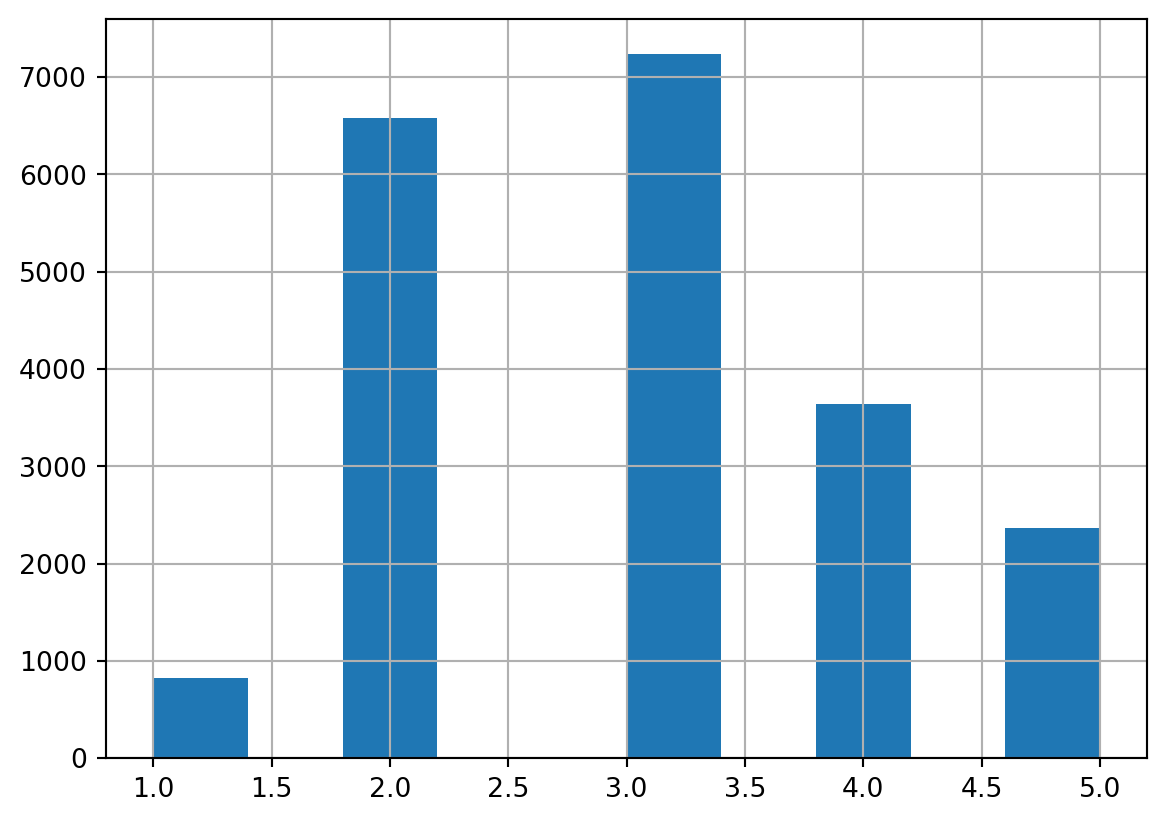
labels=[1, 2, 3, 4, 5])In order to do that we need to define the bins and assign labels to each bin. Where label 1 indicates the low income group, label 2 indicates income between zero and 1.5, etc. We can then plot histograms of this new categorical variable.
print(housing["income_cat"].value_counts())
housing["income_cat"].hist()3 7236
2 6581
4 3639
5 2362
1 822
Name: income_cat, dtype: int64When we split the sample into a training set and a test set we need to make sure that the distribution of the different income groups is maintained in the subsamples. We want to avoid as situation where we have, let’s say richer households in the training sample and relatively poorer households in the testing sample. We can accomplish this with stratified sampling. The built in command StratifiedShuffleSplit will split the data ensuring that the distribution is maintained.
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]We can check this by comparing the histogram we made earlier for the entire data with the histogram for the income variables of the stratified test sample. You see that the proportions of the different income groups are maintained because we split the sample according to the income strata in the above code block.
print(strat_test_set["income_cat"].value_counts() / len(strat_test_set))3 0.350533
2 0.318798
4 0.176357
5 0.114341
1 0.039971
Name: income_cat, dtype: float64We can compare it to the income categories of the original data.
print(housing["income_cat"].value_counts() / len(housing))3 0.350581
2 0.318847
4 0.176308
5 0.114438
1 0.039826
Name: income_cat, dtype: float64We next do it more systematic across the full data, the stratified test set, and the non-stratified test set. We then plot the proportions of the income groups for each data set. You want the proportions in the test set be very close to the income proportions in the full data.
def income_cat_proportions(data):
return data["income_cat"].value_counts() / len(data)
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
compare_props = pd.DataFrame({
"Overall": income_cat_proportions(housing),
"Stratified": income_cat_proportions(strat_test_set),
"Random": income_cat_proportions(test_set),
}).sort_index()
compare_props["Rand. %error"] = 100 * compare_props["Random"] / compare_props["Overall"] - 100
compare_props["Strat. %error"] = 100 * compare_props["Stratified"] / compare_props["Overall"] - 100Now let’s have a look at the different methods and how they compare to the original data.
print(compare_props) Overall Stratified Random Rand. %error Strat. %error
1 0.039826 0.039971 0.040213 0.973236 0.364964
2 0.318847 0.318798 0.324370 1.732260 -0.015195
3 0.350581 0.350533 0.358527 2.266446 -0.013820
4 0.176308 0.176357 0.167393 -5.056334 0.027480
5 0.114438 0.114341 0.109496 -4.318374 -0.084674Before we move on, we drop the income category variable because we do not use this categorical variable in our “forecasting” model.
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis=1, inplace=True)15.1.4 Visualize data to gain insight
We next copy the stratified training data set and assign it a shorter name.
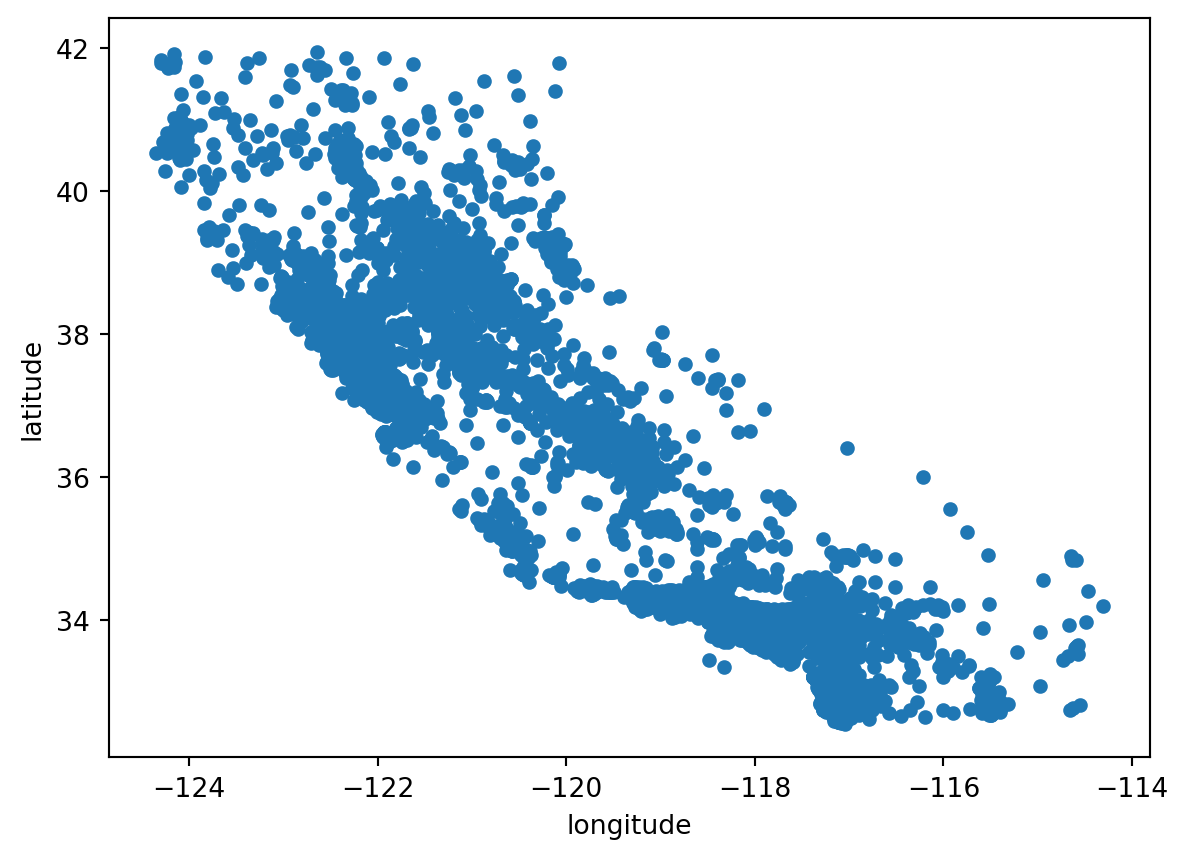
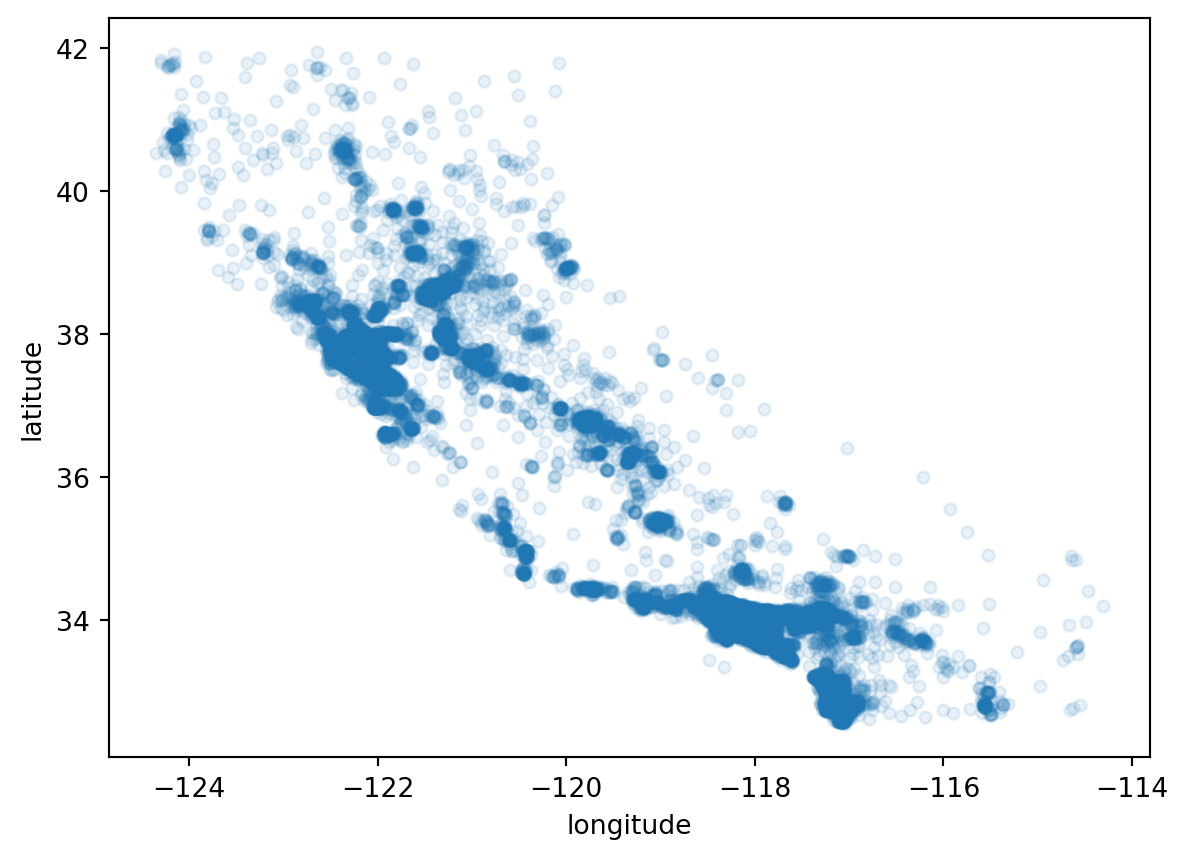
housing = strat_train_set.copy()We next make a scatter splot to get a feel for the geographic location of the house observations. Once we plot it, we roughly see the outline of the State of California.
We can do a little better by making the data points in the graph a bit opaque using the alpha option in the plot command. This option allows us to specify the “opaqueness” of the dots in the scatterplot.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
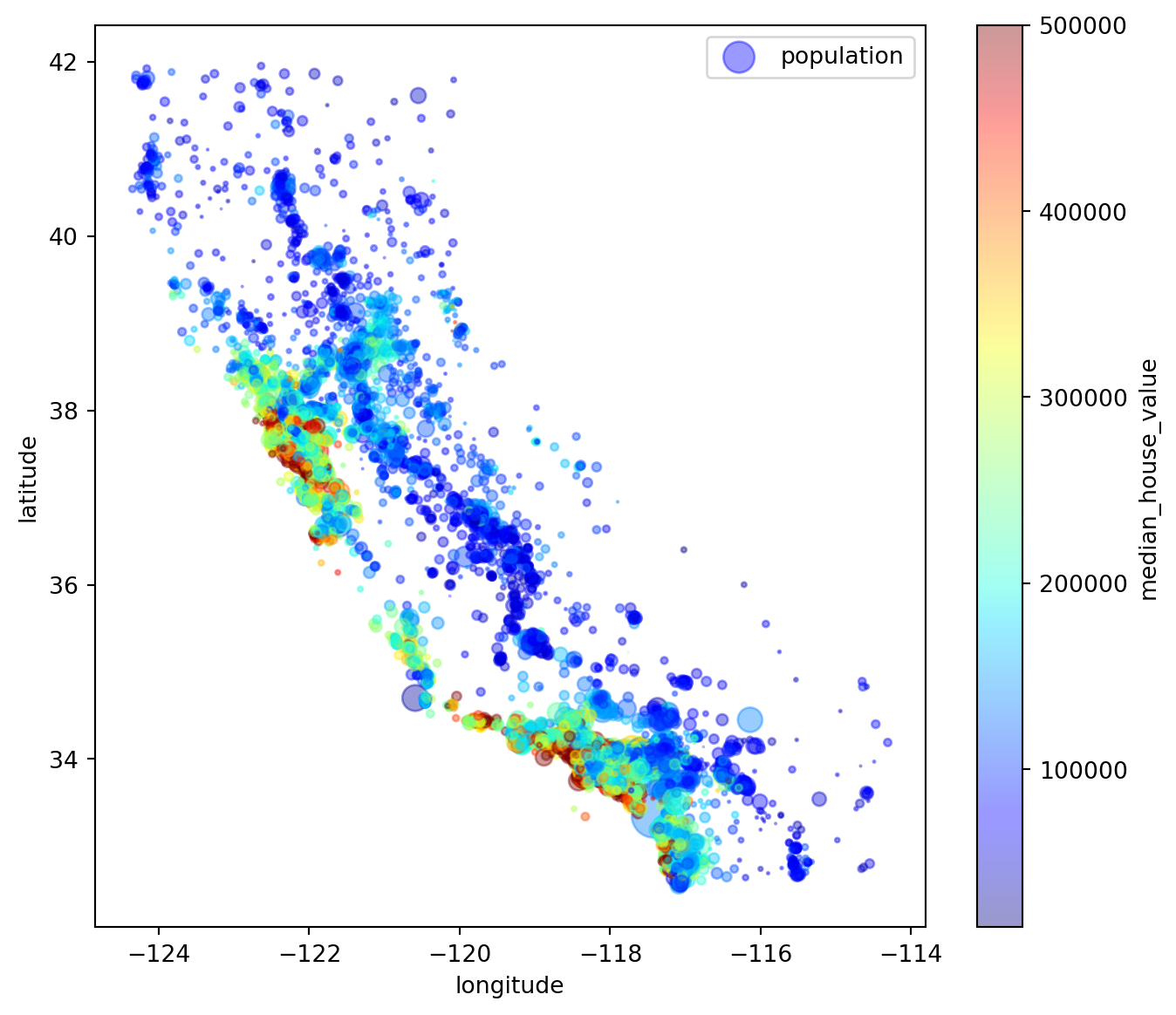
# save_fig("better_visualization_plot")We can also adjust the data point size using a population measure. So a bigger point represents a housing observation from a place with a higher population density.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(8,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
sharex=False)
plt.legend()
# save_fig("housing_prices_scatterplot")We next investigate correlations between the value of the house and the other variables in our data in order to get a feel for what a good forecasting model should factor in.
corr_matrix = housing.corr(numeric_only=True)
print(corr_matrix["median_house_value"].sort_values(ascending=False))median_house_value 1.000000
median_income 0.687151
total_rooms 0.135140
housing_median_age 0.114146
households 0.064590
total_bedrooms 0.047781
population -0.026882
longitude -0.047466
latitude -0.142673
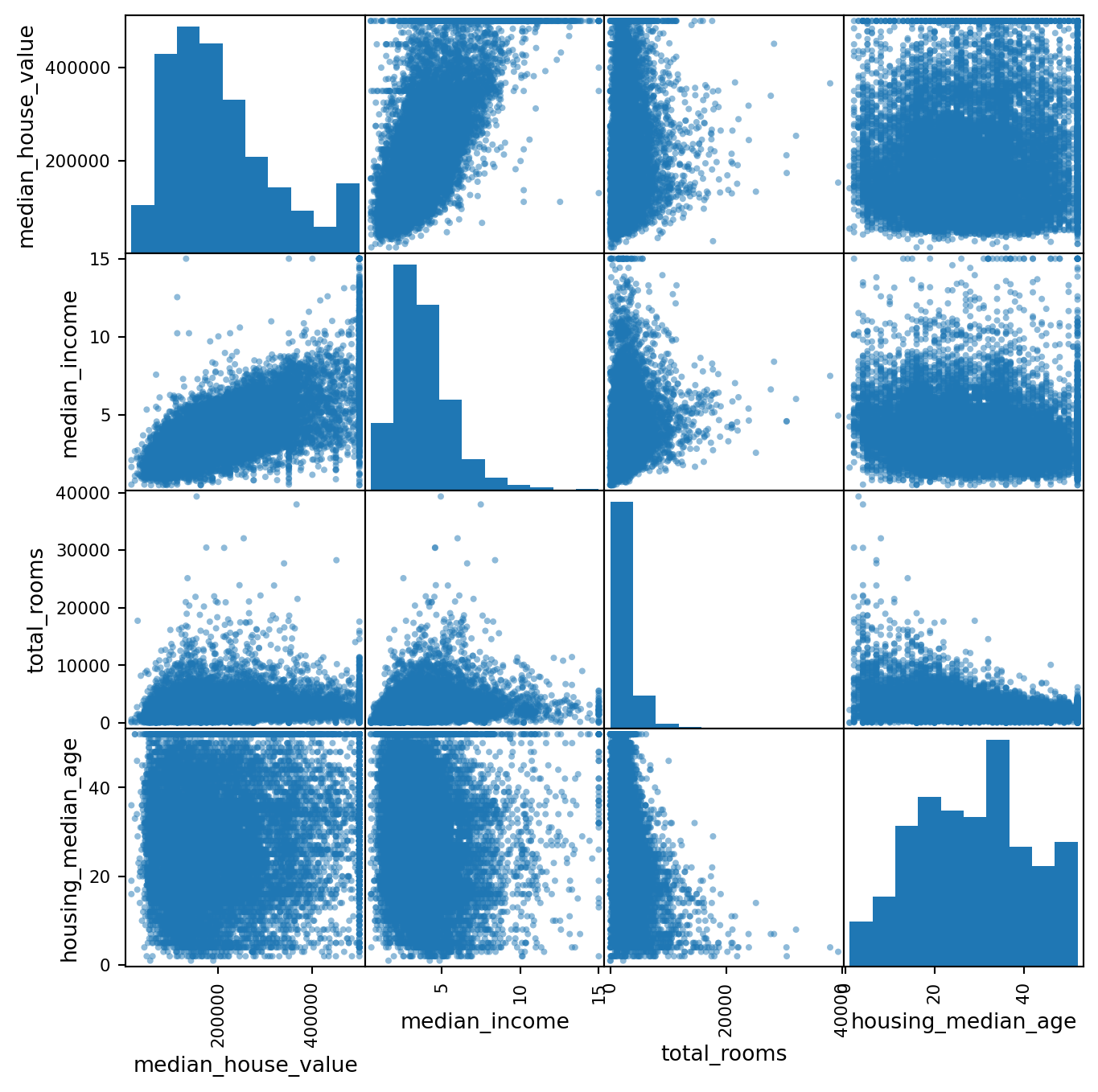
Name: median_house_value, dtype: float64The Pandas library has a very powerful command that allows you to draw scatter plots for all variable combinations. This is a visual method to inspect the correlation between variables.
# from pandas.tools.plotting import scatter_matrix # For older versions of Pandas
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(housing[attributes], figsize=(8, 8))
# save_fig("scatter_matrix_plot")array([[<Axes: xlabel='median_house_value', ylabel='median_house_value'>,
<Axes: xlabel='median_income', ylabel='median_house_value'>,
<Axes: xlabel='total_rooms', ylabel='median_house_value'>,
<Axes: xlabel='housing_median_age', ylabel='median_house_value'>],
[<Axes: xlabel='median_house_value', ylabel='median_income'>,
<Axes: xlabel='median_income', ylabel='median_income'>,
<Axes: xlabel='total_rooms', ylabel='median_income'>,
<Axes: xlabel='housing_median_age', ylabel='median_income'>],
[<Axes: xlabel='median_house_value', ylabel='total_rooms'>,
<Axes: xlabel='median_income', ylabel='total_rooms'>,
<Axes: xlabel='total_rooms', ylabel='total_rooms'>,
<Axes: xlabel='housing_median_age', ylabel='total_rooms'>],
[<Axes: xlabel='median_house_value', ylabel='housing_median_age'>,
<Axes: xlabel='median_income', ylabel='housing_median_age'>,
<Axes: xlabel='total_rooms', ylabel='housing_median_age'>,
<Axes: xlabel='housing_median_age', ylabel='housing_median_age'>]],
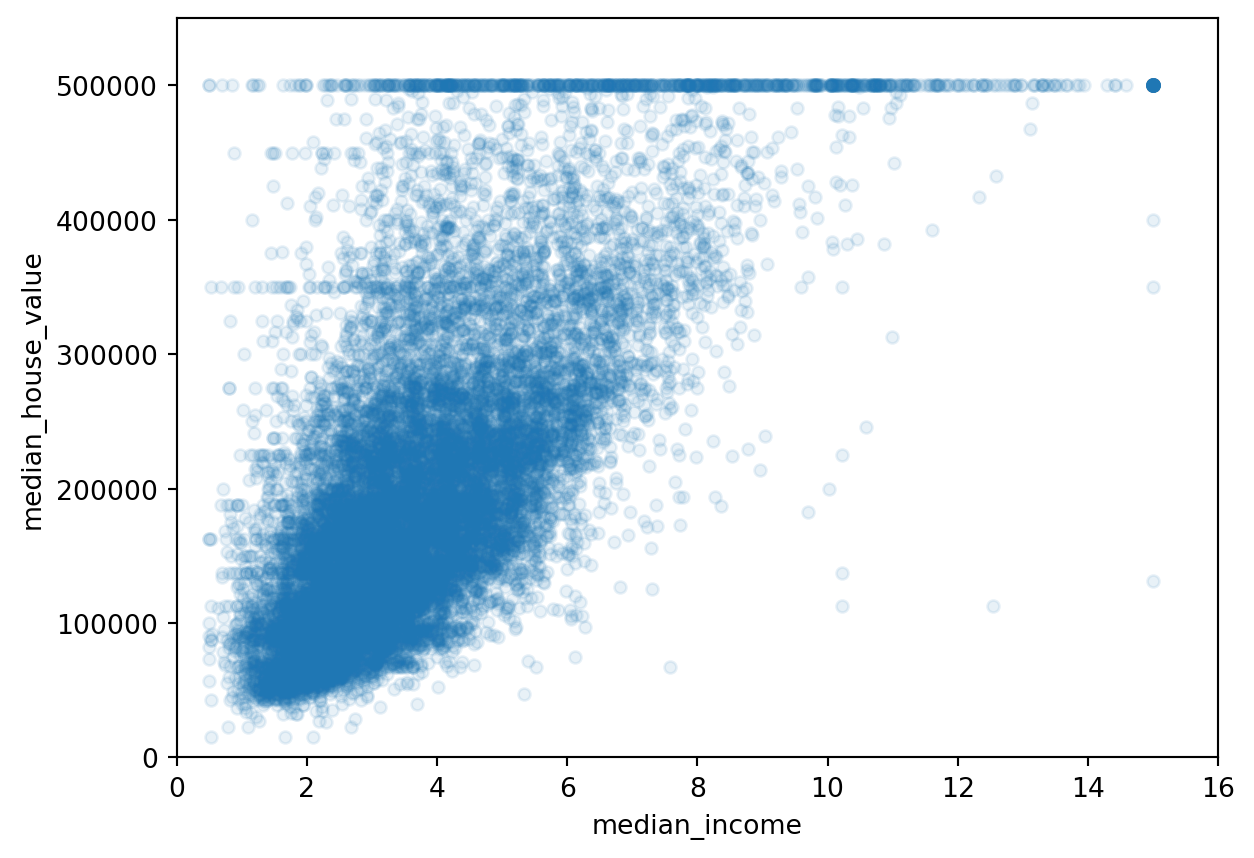
dtype=object)housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1)
plt.axis([0, 16, 0, 550000])
# save_fig("income_vs_house_value_scatterplot")Finally we can generate some additional variables that are combinations of variables in our original data set.
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]
# Note: there was a bug in the previous cell, in the definition of the rooms_per_household attribute. This explains why the correlation value below differs slightly from the value in the book (unless you are reading the latest version).
corr_matrix = housing.corr(numeric_only=True)
print(corr_matrix["median_house_value"].sort_values(ascending=False))median_house_value 1.000000
median_income 0.687151
rooms_per_household 0.146255
total_rooms 0.135140
housing_median_age 0.114146
households 0.064590
total_bedrooms 0.047781
population_per_household -0.021991
population -0.026882
longitude -0.047466
latitude -0.142673
bedrooms_per_room -0.259952
Name: median_house_value, dtype: float6415.1.5 Prepare data
Before training (estimating) the model we need to prepare the data for the built in Machine Learning algorithms. We need to make sure that the data only contains numeric data and not strings, lists, etc.
We first put the label variable and the rest of the data (the X variables) into separate dataframes.
housing = strat_train_set.drop("median_house_value", axis=1) # drop labels for training set
housing_labels = strat_train_set["median_house_value"].copy()We then check how many observations with incomplete (i.e., missing) observations we have.
sample_incomplete_rows = housing[housing.isnull().any(axis=1)].head()
print(sample_incomplete_rows) longitude latitude housing_median_age total_rooms total_bedrooms \
1606 -122.08 37.88 26.0 2947.0 NaN
10915 -117.87 33.73 45.0 2264.0 NaN
19150 -122.70 38.35 14.0 2313.0 NaN
4186 -118.23 34.13 48.0 1308.0 NaN
16885 -122.40 37.58 26.0 3281.0 NaN
population households median_income ocean_proximity
1606 825.0 626.0 2.9330 NEAR BAY
10915 1970.0 499.0 3.4193 <1H OCEAN
19150 954.0 397.0 3.7813 <1H OCEAN
4186 835.0 294.0 4.2891 <1H OCEAN
16885 1145.0 480.0 6.3580 NEAR OCEAN We next run a built in function over our data that attempts to impute missing data with the median values of similar observations.
# Warning: Since Scikit-Learn 0.20, the sklearn.preprocessing.Imputer class was replaced by the sklearn.impute.SimpleImputer class.
try:
from sklearn.impute import SimpleImputer # Scikit-Learn 0.20+
except ImportError:
from sklearn.preprocessing import Imputer as SimpleImputer
imputer = SimpleImputer(strategy="median")Before we run the imputing algorithm we need to remove variables from the dataframe that are not numeric such as categorical variables.
- If you would like to use categorical variables as regressors, you need to
-
make dummy variables for each of the categories of your categorical variable. In other words, you need to code up a categorical variable as a (dummy set of) numerical variables so that you can “do math” with your categorical variable information.
# Remove the text attribute because median can only be calculated on numerical attributes:
housing_num = housing.drop('ocean_proximity', axis=1)
# alternatively: housing_num = housing.select_dtypes(include=[np.number])
imputer.fit(housing_num)
print(imputer.statistics_)
print(housing_num.median().values)[-118.51 34.26 29. 2119. 433. 1164.
408. 3.54155]
[-118.51 34.26 29. 2119. 433. 1164.
408. 3.54155]X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns=housing_num.columns,
index=housing.index)
print(housing_tr.head()) longitude latitude housing_median_age total_rooms total_bedrooms \
12655 -121.46 38.52 29.0 3873.0 797.0
15502 -117.23 33.09 7.0 5320.0 855.0
2908 -119.04 35.37 44.0 1618.0 310.0
14053 -117.13 32.75 24.0 1877.0 519.0
20496 -118.70 34.28 27.0 3536.0 646.0
population households median_income
12655 2237.0 706.0 2.1736
15502 2015.0 768.0 6.3373
2908 667.0 300.0 2.8750
14053 898.0 483.0 2.2264
20496 1837.0 580.0 4.4964 We have now created a complete dataset with no more missing observations that only contains numeric variables.
We next need to handle the categorical variable of ocean proximity of a housing unit. Let us inspect this variable first.
housing_cat = housing[['ocean_proximity']]
housing_cat.head(10)| ocean_proximity | |
|---|---|
| 12655 | INLAND |
| 15502 | NEAR OCEAN |
| 2908 | INLAND |
| 14053 | NEAR OCEAN |
| 20496 | <1H OCEAN |
| 1481 | NEAR BAY |
| 18125 | <1H OCEAN |
| 5830 | <1H OCEAN |
| 17989 | <1H OCEAN |
| 4861 | <1H OCEAN |
We next use a label encoder function which is part of the sklearn toolkit. This is basically a function that will generate dummy variables out of categorical variables. Dummy variables are variables that are either 0 or 1 and and it can be used to encode categorical (i.e., non numerical attributes) such as gender. The dummy variable could be called d_female. It is equal to 1 if a person is female and 0 if a person is not female.
The ocean proximity variable has multiple categories in it, not just two as in the gender example. For each category of the ocean proximity variable we have to create a dummy variable. We could accomplish this separately for each dummy variable using if statements or we can use the built in OrdinalEncoder to do it in one line of code.
Some earlier machine learning codes used the LabelEncoder class or Pandas’ Series.factorize() method to encode string categorical attributes as integers. However, the OrdinalEncoder class that was introduced in Scikit-Learn 0.20 (see PR #10521) is preferable since it is designed for input features (X instead of labels y) and it plays well with pipelines (introduced later). If you are using an older version of Scikit-Learn (<0.20), then you can import it from future_encoders.py instead.
try:
# New version of categorial variable encoder
from sklearn.preprocessing import OrdinalEncoder
except ImportError:
# Use old version, if new version of categorial variable encoder fails
from future_encoders import OrdinalEncoder # Scikit-Learn < 0.20
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
print(housing_cat_encoded[:10])
print(ordinal_encoder.categories_)[[1.]
[4.]
[1.]
[4.]
[0.]
[3.]
[0.]
[0.]
[0.]
[0.]]
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]We have now encoded a string categorical variable into numerical values. However, before we run regressions, we need to make dummy variables out of a categorical variable (no matter whether it’s a string category or numeric categories). The reason is that the machine learning algorithm will assume that two nearby values are more similar than two distant values. This is okay if your categories are “bad”, “average”, “good”, and “excellent”, but it is not thecase for the ocean_proximity variable above where categories 0 and 4 are clearly more similar than categories 0 and 1.
We therefore resort to one-hot encoding, where a for each category we make a separate variable. Let us pick one category out of the ocean_proximity column, say “<1H OCEAN”. For this category we create a new column that we encode as 1 (hot) if the house is less than one our from the ocean and 0(cold) otherwise. This is also called a dummy variable.
Older machine learning codes used the LabelBinarizer or CategoricalEncoder classes to convert each categorical value to a one-hot vector (i.e., a dummy 0/1 variable). It is now preferable to use the OneHotEncoder class. Since Scikit-Learn 0.20 it can handle string categorical inputs (see PR #10521), not just integer categorical inputs. If you are using an older version of Scikit-Learn, you can import the new version from future_encoders.py:
try:
from sklearn.preprocessing import OrdinalEncoder # just to raise an ImportError if Scikit-Learn < 0.20
from sklearn.preprocessing import OneHotEncoder
except ImportError:
from future_encoders import OneHotEncoder # Scikit-Learn < 0.20
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
print(housing_cat_1hot)
print(cat_encoder.categories_) (0, 1) 1.0
(1, 4) 1.0
(2, 1) 1.0
(3, 4) 1.0
(4, 0) 1.0
(5, 3) 1.0
(6, 0) 1.0
(7, 0) 1.0
(8, 0) 1.0
(9, 0) 1.0
(10, 1) 1.0
(11, 0) 1.0
(12, 1) 1.0
(13, 1) 1.0
(14, 4) 1.0
(15, 0) 1.0
(16, 0) 1.0
(17, 0) 1.0
(18, 3) 1.0
(19, 0) 1.0
(20, 1) 1.0
(21, 3) 1.0
(22, 1) 1.0
(23, 0) 1.0
(24, 1) 1.0
: :
(16487, 1) 1.0
(16488, 0) 1.0
(16489, 4) 1.0
(16490, 4) 1.0
(16491, 1) 1.0
(16492, 1) 1.0
(16493, 0) 1.0
(16494, 0) 1.0
(16495, 0) 1.0
(16496, 1) 1.0
(16497, 0) 1.0
(16498, 4) 1.0
(16499, 0) 1.0
(16500, 0) 1.0
(16501, 1) 1.0
(16502, 1) 1.0
(16503, 1) 1.0
(16504, 1) 1.0
(16505, 0) 1.0
(16506, 0) 1.0
(16507, 0) 1.0
(16508, 1) 1.0
(16509, 0) 1.0
(16510, 0) 1.0
(16511, 1) 1.0
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]We next use Scikit-Learn’s FunctionTransformer class that lets you easily create a transformer based on a transformation function. Note that we need to set validate=False because the data contains non-float values (validate will default to False in Scikit-Learn 0.22).
# get the right column indices: safer than hard-coding indices 3, 4, 5, 6
rooms_ix, bedrooms_ix, population_ix, household_ix = [
list(housing.columns).index(col)
for col in ("total_rooms", "total_bedrooms", "population", "households")]from sklearn.preprocessing import FunctionTransformer
def add_extra_features(X, add_bedrooms_per_room=True):
rooms_per_household = X[:, rooms_ix] / X[:, household_ix]
population_per_household = X[:, population_ix] / X[:, household_ix]
if add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household,
bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = FunctionTransformer(add_extra_features, validate=False,
kw_args={"add_bedrooms_per_room": False})
housing_extra_attribs = attr_adder.fit_transform(housing.values)
print(housing_extra_attribs[0:3,:])[[-121.46 38.52 29.0 3873.0 797.0 2237.0 706.0 2.1736 'INLAND'
5.485835694050992 3.168555240793201]
[-117.23 33.09 7.0 5320.0 855.0 2015.0 768.0 6.3373 'NEAR OCEAN'
6.927083333333333 2.6236979166666665]
[-119.04 35.37 44.0 1618.0 310.0 667.0 300.0 2.875 'INLAND'
5.3933333333333335 2.223333333333333]]housing_extra_attribs = pd.DataFrame(
housing_extra_attribs,
columns=list(housing.columns)+["rooms_per_household", "population_per_household"],
index=housing.index)
housing_extra_attribs.head()
print(housing_extra_attribs.head()) longitude latitude housing_median_age total_rooms total_bedrooms \
12655 -121.46 38.52 29.0 3873.0 797.0
15502 -117.23 33.09 7.0 5320.0 855.0
2908 -119.04 35.37 44.0 1618.0 310.0
14053 -117.13 32.75 24.0 1877.0 519.0
20496 -118.7 34.28 27.0 3536.0 646.0
population households median_income ocean_proximity rooms_per_household \
12655 2237.0 706.0 2.1736 INLAND 5.485836
15502 2015.0 768.0 6.3373 NEAR OCEAN 6.927083
2908 667.0 300.0 2.875 INLAND 5.393333
14053 898.0 483.0 2.2264 NEAR OCEAN 3.886128
20496 1837.0 580.0 4.4964 <1H OCEAN 6.096552
population_per_household
12655 3.168555
15502 2.623698
2908 2.223333
14053 1.859213
20496 3.167241 from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('attribs_adder', FunctionTransformer(add_extra_features, validate=False)),
('std_scaler', StandardScaler()),
])
housing_num_tr = num_pipeline.fit_transform(housing_num)try:
from sklearn.compose import ColumnTransformer
except ImportError:
from future_encoders import ColumnTransformer # Scikit-Learn < 0.20
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)
print(housing_prepared[:3,:])[[-0.94135046 1.34743822 0.02756357 0.58477745 0.64037127 0.73260236
0.55628602 -0.8936472 0.01739526 0.00622264 -0.12112176 0.
1. 0. 0. 0. ]
[ 1.17178212 -1.19243966 -1.72201763 1.26146668 0.78156132 0.53361152
0.72131799 1.292168 0.56925554 -0.04081077 -0.81086696 0.
0. 0. 0. 1. ]
[ 0.26758118 -0.1259716 1.22045984 -0.46977281 -0.54513828 -0.67467519
-0.52440722 -0.52543365 -0.01802432 -0.07537122 -0.33827252 0.
1. 0. 0. 0. ]]15.1.6 Training a Regression Model
#%% Select and train a model
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
# let's try the full preprocessing pipeline on a few training instances
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions:", lin_reg.predict(some_data_prepared))
print("Lables:", list(some_labels))Predictions: [ 85657.90192014 305492.60737488 152056.46122456 186095.70946094
244550.67966089]
Lables: [72100.0, 279600.0, 82700.0, 112500.0, 238300.0]from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)68627.87390018743from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(housing_labels, housing_predictions)
print(lin_mae)49438.66860915803Machine learning
- The basics
- Why is regression analysis machine learning. What type of machine learning is it?